問 題
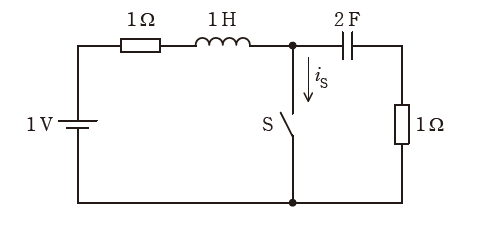
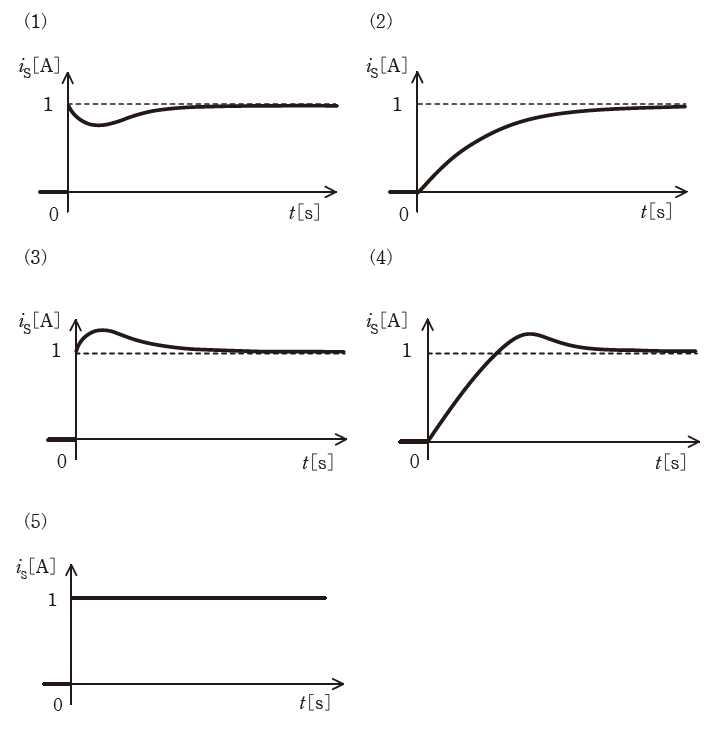
図の回路のスイッチSをt=0sで閉じる。電流iS[A]の波形として最も適切に表すものを次の(1)~(5)のうちから一つ選べ。
ただし、スイッチSを閉じる直前に、回路は定常状態にあったとする。
解 説
本問の場合、スイッチSを閉じる直前の状態ではコンデンサの充電が完了しているため、コンデンサは「開放」状態であり、この回路には周回できる部分が一切ないので、どこにも電流は流れていません。
ここでSを閉じた瞬間に、コイルを含む左半分の回路に電流が流れるようになり、一方でコンデンサを含む右半分の回路もコンデンサが放電を始めるので電流が流れるようになります。
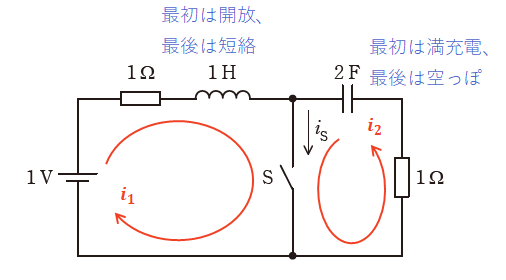
まずは回路の左半分について考えると、電流が流れ始めた瞬間のコイルの両端の電位差は大きく、電流は全然流れません。その後、徐々に電位差が小さくなり(=電流が大きくなっていき)、充分な時間が経ったあとのコイルは、その両端の電位差が0になります。
つまり、コイルは電流が流れた瞬間は「開放」で、定常状態では「短絡」しているものと見なすことができるので、ここを流れる電流i1[A]は、時間経過とともに次のような軌跡を描きます。
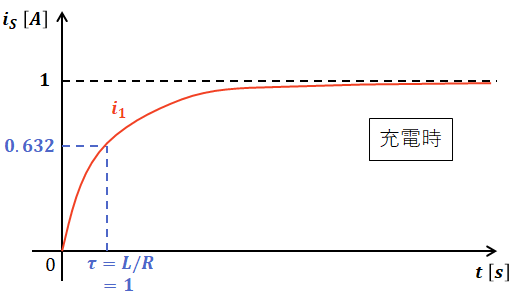
上図において、充電時に電流i1が最大値の63.2%になるまでに掛かる時間を時定数τといい、RL直列回路ではτ=L/Rで表されます。
一方、回路の右半分について考えると、充電が完了していたコンデンサは、最初は電源と同じように勢いよく放電しますが、徐々に電流が弱まり、放電し切ったあとは電流が流れなくなります。よって、ここを流れる電流i2[A]は、時間経過とともに次のような軌跡を描きます。
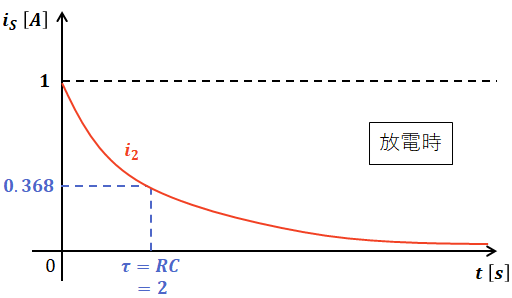
上図において、放電時は電流i2が最大値の36.8%(=100-63.2)になるまでに掛かる時間が時定数τであり、RC直列回路ではτ=RCで表されます。
以上から、両方を合わせて考えると、スイッチを流れる電流iS=i1+i2[A]は、以下のように常に一定の値となります。
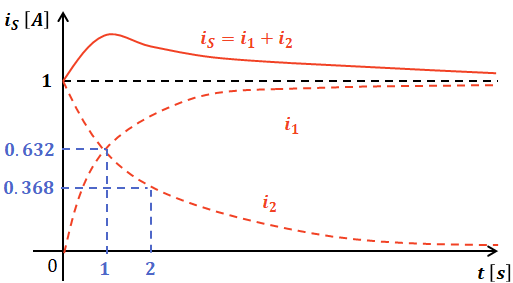
よって、正解は(3)です。

コメント