電験三種 R6年度上期 理論 問8 問題と解説

　問 題　　　　　

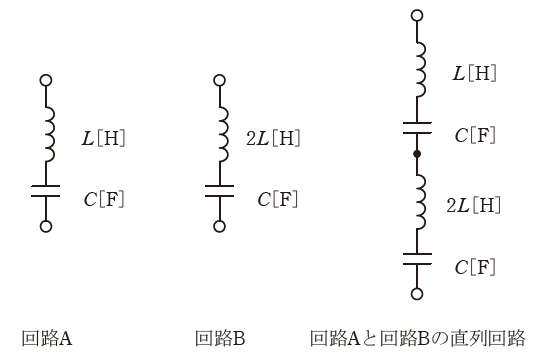
図のように、二つのLC直列共振回路A、Bがあり、それぞれの共振周波数がf_A[Hz]、f_B[Hz]である。これらA、Bをさらに直列に接続した場合、全体としての共振周波数がf_AB[Hz]になった。

f_A、f_B及びf_ABの大小関係として、正しいものを次の(1)～(5)のうちから一つ選べ。

1. f_A  ＜ f_B  ＜ f_AB
2. f_A  ＜ f_AB ＜ f_B
3. f_B  ＜ f_AB ＜ f_A
4. f_AB ＜ f_A  ＜ f_B
5. f_AB ＜ f_B  ＜ f_A

 

 

 

 

 

　解 説　　　　　

LC直列共振回路では、コイルのリアクタンスとコンデンサのリアクタンスが同じ大きさ(符号は反対)になります。よって、共振周波数f_A、f_Bはそれぞれ次のように計算することができます。

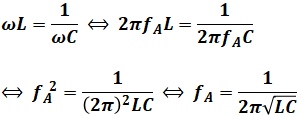
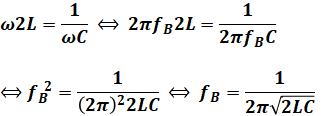
また、回路Aと回路Bの直列接続では、コイルのインダクタンスは単純に和で求められるので今回はL+2L=3Lとなり、コンデンサの静電容量は逆数の和が静電容量の和になるので、(1/C)+(1/C)=(2/C)より、合成した値はC/2となります。よって、共振周波数f_ABは次のように計算できます。

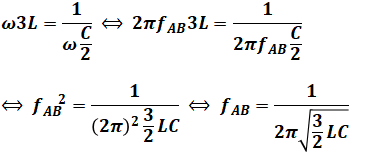
以上から、3つの共振周波数を比べると、分母のLCの係数がf_A、f_B、f_ABの順に1、2、1.5であり、分母が大きいほど全体は小さくなるので、共振周波数の大小関係は「f_B＜f_AB＜f_A」となります。

よって、正解は(3)です。