電験三種 R6年度上期 理論 問7 問題と解説

　問 題　　　　　

起電力がE[V]で内部抵抗がr[Ω]の電池がある。この電池に抵抗R₁[Ω]と可変抵抗R₂[Ω]を並列につないだとき、抵抗R₂[Ω]から発生するジュール熱が最大となるときの抵抗R₂の値[Ω]を表す式として、正しいものを次の(1)～(5)のうちから一つ選べ。

 

 

 

 

 

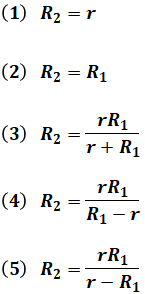
　解 説　　　　　

この問題はやや難易度の高い問題です。直列回路であればまだしも、並列回路になると微分を使わないと正確な計算をするのが難しいです。そのため、ご自身の学習状況や理解度によっては後回しにしても構わないと思います。

なお、電験三種試験で微分・積分の知識が必要となる機会はほとんどないため、ここでは微分を使わない解法を紹介します。

まず、電池には起電力Eと内部抵抗rがあり、外部には抵抗R₁と可変抵抗R₂が並列に接続されています。

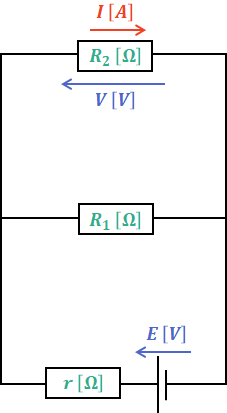
ここで、R₁とR₂の合成抵抗R₁₂は次の(1)式のように表すことができます。

また、R₁₂の端子間電圧V(＝R₂の端子間電圧)は、回路全体の抵抗(r＋R₁₂)のうちのR₁₂側の分に相当するため、次の(2)式のようになります。

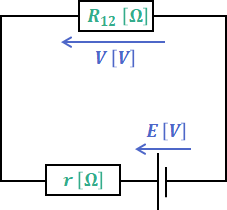
よって、R₂に流れる電流Iは次に示す(3)式で表すことができるため、R₂で発生するジュール熱Pは(4)式のようになります。

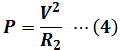
この(4)式で表したPが最大になるのは、R₂が大きすぎず小さすぎず、ちょうどよい値のときです。

というのも、もしR₂があまりにも小さいと、(1)式で示した合成抵抗R₁₂は小さくなり、結果として(2)式で表される端子間電圧Vも低くなります。低い電圧では、たとえ(4)式の右辺の分母であるR₂自体が小さいとはいえ、分子にある2乗が効いて、全体としてPの値が十分な大きさになりません。

逆に、もしR₂があまりにも大きいと、(1)式のR₁₂はほぼR₁と同じ値になり、(2)式のVが定数のように見なせます。つまり、(4)式の右辺の分子が一定の数であるのに対して分母が大きくなるため、やはり全体としてPの値が小さくなってしまいます。

このように、R₂の値が小さすぎる場合と大きすぎる場合、どちらもジュール熱が十分に発生しない原因となります。

以下では、その間のちょうどバランスが取れるところについて考えます。きちんと解こうとすると解説の冒頭に示した通り微分を用いる必要があるため、ここではテクニック(または直感)に頼ることになります。

ここで、(2)式に(1)式を代入して、変数であるR₂を含む項と含まない項に分けて整理していくと、次に示す(5)式のように書くことができます。

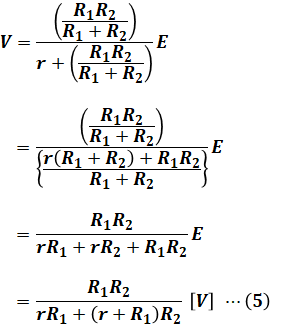
(5)式の分母に注目すると、内部抵抗に関連する定数項が「rR₁」、R₂に応じて変化する変数項が「(r＋R₁)R₂」となっています。このような場合、両者のバランスが最も取れるのは、これら2つの項が同じ大きさになったときと考えることができます。

よって、以下で示す(6)式が成り立ちます。

この式をR₂について解けば、ジュール熱Pが最大となるR₂の式を求めることができます。

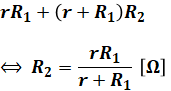
以上から、正解は(3)となります。