電験三種 R6年度上期 理論 問4 問題と解説

　問 題　　　　　

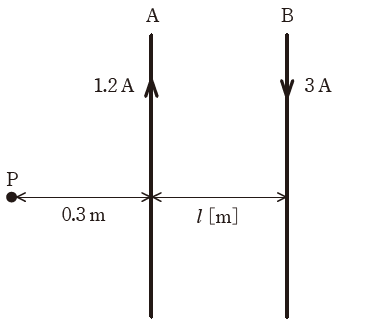
図のように、A、B 2本の平行な直線導体があり、導体Aには1.2Aの、導体Bにはそれと反対方向に3Aの電流が流れている。導体AとBの間隔がl[m]のとき、導体Aより0.3m離れた点Pにおける合成磁界が零になった。

lの値[m]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、導体A、Bは無限長とし、点Pは導体A、Bを含む平面上にあるものとする。

1. 0.24
2. 0.45
3. 0.54
4. 0.75
5. 1.05

 

 

 

 

 

　解 説　　　　　

無限に長い直線状導体に直流電流を流すと、下図のようにその電流に応じた強さの磁界が導体の周りに円を描くように発生します。

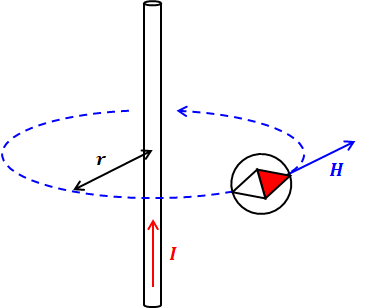
このとき、直線導体を流れる電流がつくる磁界Hは、以下の(1)式で表されます。この式は重要公式としてぜひ押さえておきたい知識です。

• H：磁界 [A/m]
• I：電流 [A]
• r：導体と磁界の距離 [m]

また、磁界には向きがあります。上図の通り、電流が画面下から画面上に流れている場合、磁界の向きは(上から見て)反時計回りとなります。これは、右ねじの法則に従っています。

以上を踏まえて問題文を見ると、導体A、Bを流れる電流の向きは互いに反対方向であるので、発生する磁界の向きも反対方向となります。

よって、点Pでの合成磁界が零であるということは、点Pにおいて、導体Aが作る磁界と導体Bが作る磁界の大きさが等しいことがわかります(向きは反対)。

そのため、A、Bそれぞれの条件を(1)式に当てはめ、それらを等式で結んでlについて解けば、求めたい答えが得られます。

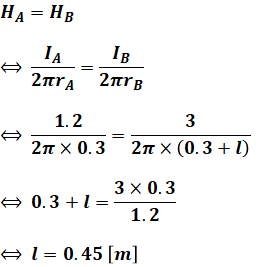
以上から、正解は(2)となります。