問 題
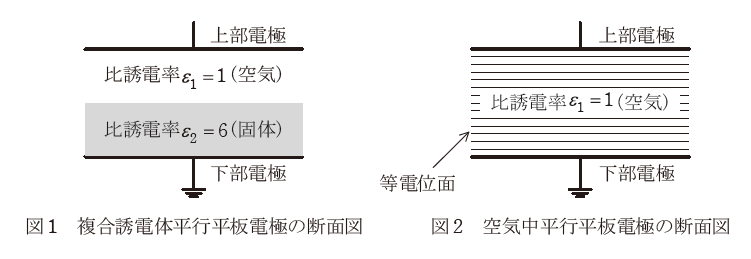
図1に示すような、空気を含む二つの誘電体からなる平行平板電極がある。この下部電極を接地し、上部電極に電圧を加えたときの電極間の等電位線の分布を示す断面図として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、誘電体の導電性及び電極と誘電体の端効果は無視できるものとする。
参考までに固体誘電体を取り除いた、空気中平行平板電極の場合の等電位線の分布を図2に示す。

正解 (5)
解 説
本問は、上下2枚の平行平板電極の間に空気(ε1=1)と固体誘電体(ε2=6)が直列に配置された場合の等電位線の分布を問う問題です。
以下の解説では、ε1とε2に合わせて、空気層のパラメータは○1、固体層のパラメータは○2と表します。
まず、上下2枚の平行平板電極の面積は同じと考えられるので、空気層と固体層を垂直に貫く電束密度D[C/m2]は、両層で同じ値をとります。
![]()
また、電束密度DはD=ε0εrEと書けるため、空気層(εr=ε1=1)と固体層(εr=ε2=6)では、電界Eの比は次のように表すことができます。
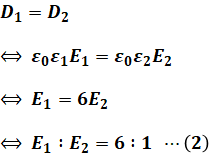
上記の(2)式から、空気層の電界は固体層の6倍大きいことがわかります。
ここで、問われているのは等電位線の分布ですが、電位差Vは電界Eと層の厚さdの積で求められます。層の厚さは図1では空気層でも固体層でも同じくらいなので、問題文には書かれていませんが、d1=d2と考えて話を進めると、以下の(3)式が成り立ちます。
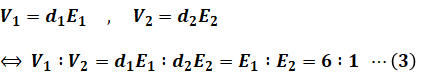
上記の(3)式より、空気層の電位差は固体層の電位差の6倍となります。よって、等電位線は上半分が密集していて下半分が疎に描かれているものが正しいといえます。より具体的には、上半分が下半分の6倍の密度となっているものが適切です。
以上から、正解は(5)となります。

コメント