電験三種 R6年度上期 機械 問14 問題と解説

　問 題　　　　　

二つのビットパターン1101と1011のビットごとの論理演算を行う。

排他的論理和(ExOR)は(　ア　)、否定論理和(NOR)は(　イ　)であり、(　ア　)と(　イ　)との論理和(OR)は(　ウ　)である。1011と(　ウ　)との排他的論理和(ExOR)の結果を2進数と考え、その数値を16進数で表すと(　エ　)である。

上記の記述中の空白箇所(ア)～(エ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

•  (ア)　　  (イ)　　  (ウ)　　(エ)

1. 1001　　0110　　1001　　9
2. 0110　　0000　　1111　　D
3. 1001　　1111　　1001　　F
4. 0110　　1111　　1001　　9
5. 0110　　0000　　0110　　D

 

 

 

 

 

　解 説　　　　　

排他的論理和(ExOR)は、2つの入力のどちらか一方が1のときだけ出力も1となるというものです。入力が2つとも0だと出力も0になり、入力が2つとも1であっても出力が0となります。

否定論理和(NOR)は、論理和(OR)を否定(反対に)したものです。

論理和は、2つの入力のうち片方でも1であれば、出力が1となるというものです。つまり、入力が両方とも0なら出力も0で、それ以外のパターンは出力が1になります。

一方、否定論理和はその反対なので、2つの入力のうち片方でも1であれば出力が0となり、入力が両方とも0のときだけ出力が1になります。

以上を踏まえると、今回の場合は下表のようになります。

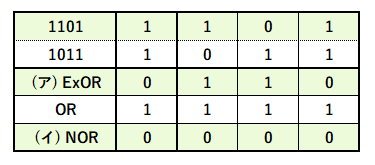
続いて、(　ア　)と(　イ　)の論理和は次の通りです。

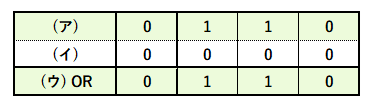
また、1011と(　ウ　)と排他的論理和は以下の表のようになります。

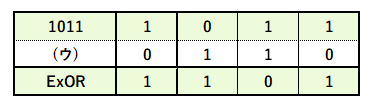
ここで、2進数の「1101」を16進数に変えると(　エ　)になりますが、直接だとわかりづらいので、いったん見慣れている10進数に直します。2進数を10進数に変換すると、次のようになります。

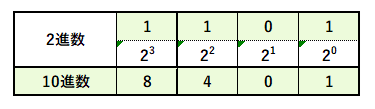
よって、これは8+4+1=13とわかります。

一方、16進数は、1桁が以下の16種類で構成されます。

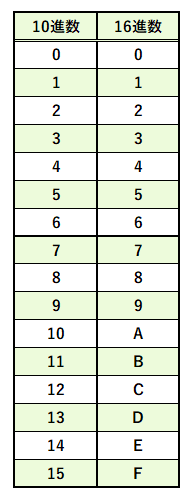
よって、(　エ　)に入るのは、10進数でいう13を16進数にしたものなので「D」です。

以上から、

• ア：0110
• イ：0000
• ウ：0110
• エ：D

となるので、正解は(5)です。