電験三種 R6年度上期 機械 問2 問題と解説

　問 題　　　　　

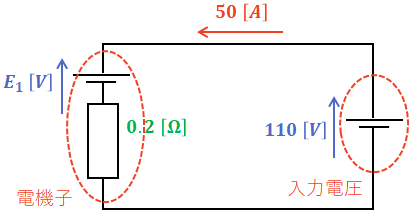
電機子回路の抵抗が0.20Ωの直流他励電動機がある。励磁電流、電機子電流とも一定になるように制御されており、電機子電流は50Aである。回転速度が1200min^－1のとき、電機子回路への入力電圧は110Vであった。

励磁電流、電機子電流を一定に保ったまま電動機の負荷を変化させたところ、入力電圧が80Vとなった。

このときの回転速度[min^－1]の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、電機子反作用はなく、ブラシの抵抗は無視できるものとする。

1. 764
2. 840
3. 873
4. 900
5. 960

 

 

 

 

 

　解 説　　　　　

この問題では直流電動機の回転速度が問われています。問題文には電圧も与えられているため、まずは次に示す直流電動機の逆起電力を表す式を確認してください。この式のパラメータには回転速度も使われています。

• E：電機子の誘導起電力 [V]
• p：磁極数
• Z：電機子総導体数
• a：巻線の並列回路数
• Φ：1極あたりの磁束 [Wb]
• n：電機子の回転速度 [min^-1]

今回は入力電圧が110[V]から80[V]に変わるという条件ですが、上式におけるp、Z、a、Φの値が変わることがありません。つまり、電機子の誘導起電力Eと回転速度nは単純な比例関係となるため、(1)式は(2)式のように簡略化できます。

ここで、まずは入力電圧が110[V]であるときの電機子の誘導起電力E₁[V]を求めます。問題文より、電機子を流れる電流が50[A]、電機子抵抗が0.20[Ω]なので、オームの法則を使うとE₁は次の(3)式のように計算することができます。

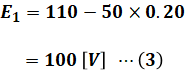
同様に、入力電圧が80[V]であるときの電機子の誘導起電力E₂[V]は次の(4)式のようになります。

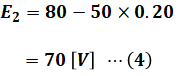
以上の(3)式と(4)式から負荷を変化させる前後の誘導起電力Eがわかりました。そして、(2)式の通りEは回転速度nに比例するため、変化後の回転速度は次のように計算することができます。

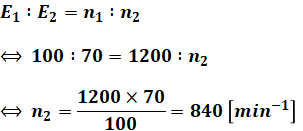
よって、正解は(2)です。