電験三種 R6年度上期 法規 問11 問題と解説

　問 題　　　　　

変電所から三相3線式1回線の専用配電線で受電している需要家がある。この配電線路の電線1条当たりの抵抗及びリアクタンスの値は、それぞれ3Ω及び5Ωである。

この需要家の使用電力が8000kW、負荷の力率が0.8(遅れ)であるとき、次の(a)及び(b)の問に答えよ。

(a)　需要家の受電電圧が20kVのとき、変電所引出口の電圧[kV]の値として、最も近いのは次のうちどれか。

1. 21.6
2. 22.2
3. 22.7
4. 22.9
5. 23.1

(b)　需要家にコンデンサを設置して、負荷の力率を0.95(遅れ)に改善するとき、この配電線の電圧降下の値[V]の、コンデンサ設置前の電圧降下の値[V]に対する比率[%]の値として、最も近いのは次のうちどれか。

ただし、この需要家の受電電圧[kV]は、コンデンサ設置前と同一の20kVとする。

1. 66.6
2. 68.8
3. 75.5
4. 81.7
5. 97.0

 

 

 

 

 

　解 説 (a)　　　

まず、問題文で与えられた条件を使って三相3線式の1相分の等価回路を描くと、以下のように表すことができます。

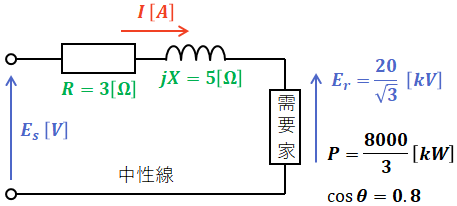
• E_s：送電端電圧(1相あたり) [V]
• E_r：受電端電圧(1相あたり) [V]
• I：線電流 [A]
• R：抵抗(電線1条あたり) [Ω]
• X：リアクタンス(電線1条あたり) [Ω]
• cosθ：力率

上図より、需要家の使用電力P[W]を表す式を使うと、電流I[A]は次の(1)式のように算出することができます。

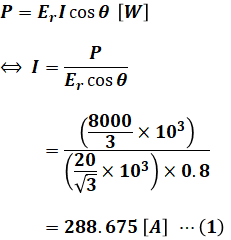
次に、三相3線式送電線における電圧降下の式は、以下の(2)式で表すことができます。これは(1)式と同様に重要公式としてそのまま覚えておきたい知識ですが、もし導出方法を知りたい場合は三相3線式送電線の電圧降下のページを参照してください。

• V_d：電圧降下 [V]
• V_s：送電端電圧 [V]
• V_r：受電端電圧 [V]
• I：線電流 [A]
• R：抵抗(電線1条あたり) [Ω]
• X：リアクタンス(電線1条あたり) [Ω]
• cosθ：負荷の力率

よって、電圧降下V_d[V]は次に示す(3)式によって計算できます。

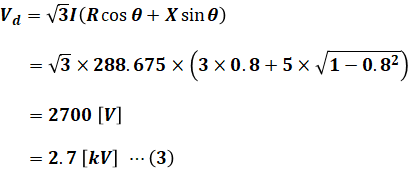
(3)式の結果を再び(2)式に代入すると、求めたい送電端電圧(変電所引出口の電圧)V_s[kV]を算出することができます。

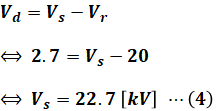
以上から、正解は(3)となります。

　解 説 (b)　　　

設問(b)ではコンデンサによって力率が0.95に上昇していますが、これは無効電力が変化しただけであり、有効電力Pは変化しません。また、問題文より受電電圧も変わっていません。

そのため、力率改善後の電流I'[A]は、設問(a)の(1)式と同じ式を使って次の(5)式のように計算することができます。

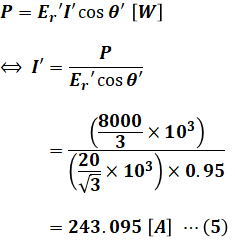
続いて、電圧降下V_d‘[V]についても、設問(a)で使った式から次の(6)式のように求めることができます。

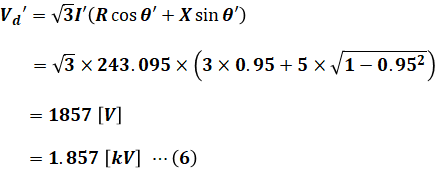
よって、(3)式と(6)式から、この配電線の電圧降下V_d‘[V]の、コンデンサ設置前の電圧降下V_d[V]に対する比率[%]は、次のように計算することができます。

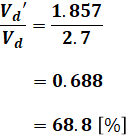
以上から、正解は(2)となります。