電験三種 R6年度上期 電力 問15 問題と解説

　問 題　　　　　

水車の種類、回転速度と比速度の関係について、次の(a)及び(b)の問に答えよ。

(a)　ある水車を有効落差200m、水車出力85000kWで運転するときの水車の比速度が100m・kWであった。

このときの水車の回転速度とこの水車に対し一般に用いられる水車の種類との組合せとして、最も適切なものを次の(1)～(5)のうちから一つ選べ。

• 　水車の種類　　回転速度[min^－1]

1. フランシス水車　　　217
2. カプラン水車　　　　217
3. カプラン水車　　　　258
4. フランシス水車　　　258
5. ペルトン水車　　　　258

(b)　この水車を同期発電機と直結し、50Hzの電力系統に接続して、同様に有効落差200m、水車出力85000kWで運転する場合、小問(a)の回転速度に最も近い回転速度で運転できる同期発電機の磁極数とそのときの回転速度による比速度の組合せとして、最も適切なものを次の(1)～(5)のうちから一つ選べ。

• 磁極数　　比速度[m・kW]

1. 　28　　　　83
2. 　28　　　　97
3. 　26　　　　89
4. 　24　　　　83
5. 　24　　　　97

 

 

 

 

 

　解 説 (a)　　　

設問(a)では「水車の種類」と「回転速度」が問われているため、まずは水車の種類について考えます。

選択肢には「フランシス水車」、「カプラン水車」、「ペルトン水車」があります。落差に注目してこれらを比較すると、それぞれ次のような特徴があります。

• ペルトン水車　：200m～1800mの高落差
• フランシス水車：40m～500mの中～やや高程度の落差
• カプラン水車　：80m以下の低落差

よって、今回はちょうど200[m]なのでペルトン水車でもぎりぎり成り立つような気もしますが、中間に位置するフランシス水車であると判断するほうが無難だといえます。

続いて、水車の比速度の公式は以下のとおりです。この式は重要ですので、ぜひ覚えておいてください。

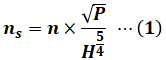
• n_s：比速度 [m・kW]
• n：水車の回転速度 [min^－1]
• P：水車の出力 [kW] (ランナorノズル1個あたりの出力)
• H：水車の有効落差 [m]

よって、(1)式に問題文で与えられているn_s、P、Hを代入して、以下に示すようにn_nについて解けば、回転速度nを算出できます。

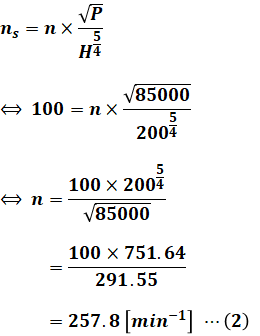
上式の計算過程における注意点として、この試験では関数電卓が使えないため、普通の電卓で5分の4乗を計算できるようになっておく必要があります。

具体的には、H＝200なので、200の√(1/2乗)を計算し、それをもう一度√に入れます。これで200の1/4乗が求まりました(約3.76)。次に、この値を5回掛ければ5乗したことになるので、一連の流れで200^5/4が計算できます(約752)。

以上から、水車の種類は「フランシス水車」、回転速度は「258」となるので、正解は(4)です。

　解 説 (b)　　　

まず、同期発電機の同期速度N_sは以下の(3)式で表すことができます。この式は特に重要な公式の一つで、これを知らないと計算が進められないことが多々あります。

• N_s：同期速度 [min^－1]
• p：磁極の数 [極]
• f：周波数 [Hz]

(3)式のうち、fは問題文より50[Hz]で、N_sは設問(a)の回転速度に近い値にしたいので、とりあえず(a)の答えである258[min^－1]を使います。すると、pは次の(4)式のように計算することができます。

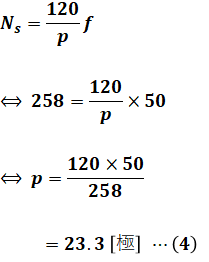
よって、この同期発電機の磁極数は、選択肢の中で最も近い値である「24」とするのが適切です。

次に比速度を求める必要があるため、設問(a)で紹介した(1)式を再び以下の(5)式として示します。先ほどと異なる数値のところは、各パラメータに「’」を付けて区別します。

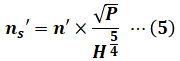
• n_s‘：比速度 [m・kW]
• n’：水車の回転速度 [min^－1]
• P：水車の出力 [kW] (ランナorノズル1個あたりの出力)
• H：水車の有効落差 [m]

上式のn_s‘を求めるためにはn’、P、Hがわかればよいですが、PとHは条件が変わっていないため、P＝85000[kW]、H＝200[m]です。

n’の回転数は、磁極数が24[極]で周波数が50[Hz]の同期速度に相当するため、(3)式で示した公式を使うと次のように計算することができます。

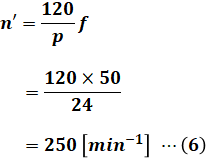
よって、これらを(5)式に代入すれば、問われているn_s‘を算出することができます。

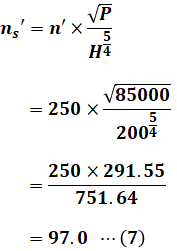
以上から、磁極数は「24」、比速度は「97」となるので、正解は(5)です。