電験三種 R6年度上期 電力 問2 問題と解説

　問 題　　　　　

総落差200m、ポンプ水車・発電電動機1台よりなる揚水発電所がある。

揚水時・発電時共に流量は100m³/s、損失水頭は揚水・発電共に総落差の2.5%、ポンプ効率・水車効率共に85%、発電効率・電動機効率共に98%とし、損失水頭及び上記4種の効率は、揚程、落差、出力、入力の変化によらず一定とする。

揚水時の電動機入力[MW]と、発電時の発電機出力[MW]の組合せとして、最も近いものを次の(1)～(5)のうちから一つ選べ。

• 電動機入力[MW]　　発電機出力[MW]

1. 　　235　　　　　　　　163
2. 　　235　　　　　　　　159
3. 　　241　　　　　　　　163
4. 　　241　　　　　　　　159
5. 　　229　　　　　　　　167

 

 

 

 

 

　解 説　　　　　

揚水発電では、まず揚水する段階では電動機とポンプを使います。つまり、電動機によって電気エネルギーを運動エネルギーに変え、ポンプによって運動エネルギーを位置エネルギーに変えます。ここで、電動機の効率(η_m)とポンプの効率(η_p)による2種類の損失が生じます。

その後、発電する段階では水車と発電機を使います。ここでも水車の効率(η_T)と発電機の効率(η_G)による2つの損失があります。

以上を踏まえて揚水時の電動機入力P₁[kW]について考えます。毎秒の揚水量をQ[m³/s]、揚げる水位をH[m]、損失水頭をh[m]とすると、理論上は次に示す(1)式のように書けます。

しかし、実際にはここに電動機の効率(η_m)とポンプの効率(η_p)が効いてくるので、次の(2)式で表されます。

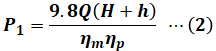
この(2)式に問題文で与えられた数値を代入して計算すると、以下の(3)式のように揚水時の電動機入力P₁[kW]を算出することができます。なお、損失水頭hは200[m]の2.5%なので5[m]です。

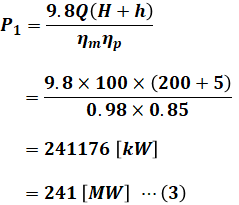
続いて、発電時の発電機出力P₂[kW]について考えます。揚水時と同様に考えると、流量Q[m³/s]、落差H[m]、損失水頭をh[m]から、理論値は次に示す(4)式のように書けます。

そして、そこに水車の効率(η_T)と発電機の効率(η_G)を加味すると、次の(5)式で表すことができます。

この(5)式に問題文で与えられた数値を代入して計算すると、以下の(6)式のように発電時の発電機出力P₂[kW]を算出することができます。

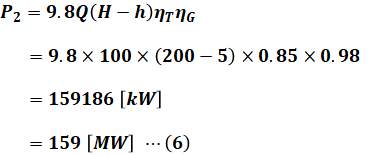
(3)式より入力が241[MW]、(6)式より出力が159[MW]なので、正解は(4)となります。