電験三種 R5年度下期 理論 問15 問題と解説

　問 題　　　　　

抵抗R[Ω]、誘導性リアクタンスX[Ω]からなる平衡三相負荷(力率80%)に対称三相交流電源を接続した交流回路がある。次の(a)及び(b)の問に答えよ。

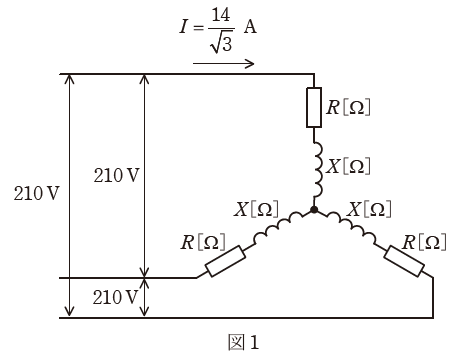
(a)　図1のように、Y結線した平衡三相負荷に線間電圧210Vの三相電圧を加えたとき、回路を流れる線電流Iは14/√3Aであった。負荷の誘導性リアクタンスXの値[Ω]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 4
2. 5
3. 9
4. 12
5. 15

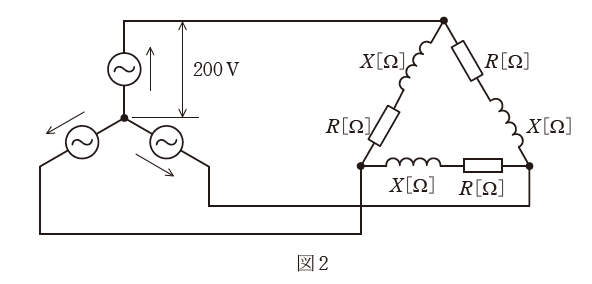
(b)　図1の各相の負荷を使ってΔ結線し、図2のように相電圧200Vの対称三相電源に接続した。この平衡三相負荷の全消費電力の値[kW]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 8
2. 11.1
3. 13.9
4. 19.2
5. 33.3

 

 

 

 

 

　解 説　　　　

(a)

問題の回路は三相回路になっていて、このままでは考えにくいので、まずは三相回路から1相分の等価回路を抜き出して考えます。なお、Y結線の場合は等価回路に仮想中性線を用いるため、等価回路1相分の電圧は線間電圧の√3分の1倍になります。

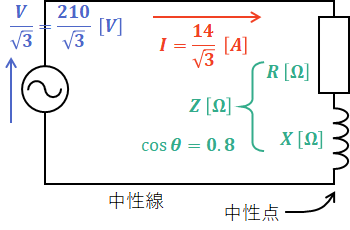
よって、この回路のインピーダンスZ[Ω]は次のように算出できます。

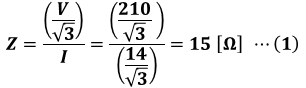
また、インピーダンス$Z[\Omega ]$は、抵抗R[Ω]と誘導性リアクタンス$X[\Omega ]を使って次のように表すこともできます。$

ここで、問題文より力率は80%(cosθ＝0.8)なので、R[Ω]は(1)式を使って次のように計算することができます。

よって、(2)式と(3)式から、問われているX[Ω]は次のように求められます。

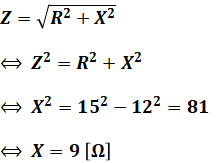
以上から、正解は(3)です。

(b)

図2は電源側がY結線で負荷側がΔ結線となっています。三相回路の計算問題ではΔ結線のままだと中性点・中性線が使えなくて計算しづらいため、Δ－Y変換によってΔ結線をY結線を変えてから等価回路を描くのが定石です。

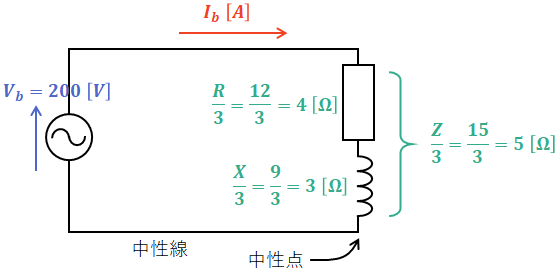
上図に示した通り、Δ－Y変換では1相あたりの抵抗やリアクタンスの値は1/3倍となります。

よって、この等価回路を流れる電流I_b[A]は次の(4)式のようになるので、この回路の消費電力P[kW]は(5)式のようになります。

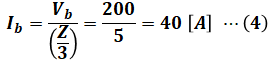
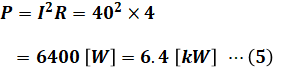
以上で1相あたりの消費電力がわかりましたが、問われているのは三相負荷の全消費電力です。よって、(5)式のP[kW]の値を3倍したものが最終的な答えとなります。

よって、正解は(4)となります。