問 題
入力信号がA、B及びC、出力信号がXの論理回路が次の真理値表を満たしているとき、Xの論理式として、正しいものを次の(1)～(5)のうちから一つ選べ。
解 説
このような問題では、全パターンの論理式を式化して考えると計算が複雑になるので、以下のようなカルノー図を使って考えるのが有効です。
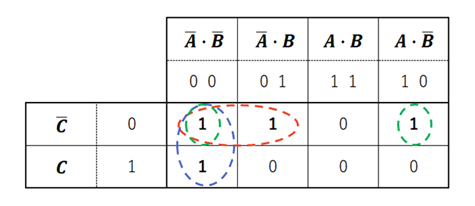
ここでは横にAとBを、縦にCを並べていますが、特にどのような組み合わせでも構いません。
カルノー図の描き方は、最初、A・Bの4つの組み合わせ(00、01、10、11)を記入し、Cも同様に2つのパターン(0、1)を書きます。その後、A・BとCの組み合わせによって4×2＝8通りのマスがありますが、問題文にある論理式を見ながら、この8マスに出力Xを0か1で入れていきます。
たとえば、問題文の真理値表の一番上は、AもBもCも0で、出力Xは1です。よって、8マスの最も左上のマスに「1」と記入できます。同様に考えていくと、8マス全てに0か1を入力していくことができます。
実際には、論理式からX＝1になるものだけを調べればよいです。あとは全て0になります(X＝0のほうだけ調べても構いません。数の少ないほうを選ぶと楽ですが、今回はX＝0とX＝1が同数なので、手間は変わりません)。
このようにしてカルノー図が描けたら、今度はこれを式化していきます。
わかりやすいのは、縦1列が全てX＝1となっている上図の青枠部分です。この部分は、
であればCに関係なく出力X＝1となることを表しています。
よって、選択肢の中で唯一がある選択肢(5)が正解だと考えられます。選択肢(1)にも
という項がありますが、この式には
が含まれていないため、不適当です。
これで正解は(5)に決まりましたが、念のため、(5)のほかの項についても確かめておきます。
(5)の第2項は
です。これは上図(カルノー図)の緑枠のところに該当します。であればAに関係なく出力X＝1となっています。同様に考えると、(5)の第3項は
なので、上図の赤枠に対応することが読み取れます。
以上から、正解は(5)となります。
コメント