電験三種 R5年度下期 電力 問15 問題と解説

　問 題　　　　　

ある需要端の負荷に対し、水力発電所1か所と重油専焼汽力発電所1か所によって電力を供給する場合において、次の(a)及び(b)の問に答えよ。

(a)　水力発電所の最大使用水量20m³/s、総落差200m、損失水頭7m、水車と発電機の総合効率85%、年間の設備利用率60%としたとき、この発電所の年間発電電力量[GW・h]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 15
2. 30
3. 170
4. 175
5. 200

(b)　需要端の負荷に供給する最大電力が100MW、年負荷率60%の場合、汽力発電所における重油の年間の消費量[kL]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、この汽力発電所の発電端熱効率は40%で運転出力に関わらず一定とする。使用する重油の発熱量は39100kJ/Lとし、発電所から需要端までの送電損失、発電所内損失は無視するものとする。

1. 13000
2. 33000
3. 82000
4. 114000
5. 120000

 

 

 

 

 

　解 説　　　　

(a)

問われているのは年間発電電力量Eの値です。これは、次の式で表すことができます。

• E：年間発電電力量 [kW・h]
• P：発電出力 [kW]
• u：年間の設備利用率
• T：1年の総時間 8760 [h]
• uT：1年間の設備利用時間 [h]

上記の(1)式において、問題文よりu＝0.6(60%)であり、Tは24時間×365日でT＝8760[h]となります。よって、Pがわかれば求めたいEの値が計算できます。

ここで、水力発電は水の位置エネルギーを電気エネルギーに変えるものなので、発電出力Pは次の式で表すことができます。

• P：発電出力 [kW]
• Q：使用水量 [m³]
• g：重力加速度 9.8 [m/s²]
• H：有効落差 [m]
• η_T：水車効率 [%]
• η_G：発電機効率 [%]

上記の(2)式において、使用水量は20[m³]であり、有効落差Hは総落差と損失水頭の差に相当するので、200－7＝193[m]となります。また、効率については総合効率ηが問題文で与えられています。よって、η＝η_Tη_G＝0.85です。

よって、(2)式を使うと発電出力Pは次のように計算することができます。(なお、ここではできるところまで計算を進めていますが、あとで(1)式と合わせるところでまとめて計算しても構いません。)

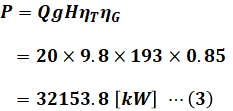
続いて、(3)式の結果を(1)式に代入すると、年間発電電力量Eの値が求められます。

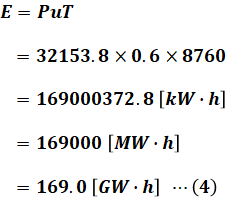
以上を踏まえて選択肢の中で最も近いものを選べばよいので、正解は(3)となります。

(b)

問われているのは汽力発電所における重油の年間の消費量[kL]です。解法の流れとしては、次のように考えていくのがわかりやすいと思います。

1. 需要端で必要となる年間電力量E_需要を計算する
2. 汽力発電で供給する年間発電量E_汽力を計算する
3. 汽力発電の入力で必要な熱エネルギーE_入力を計算する
4. 重油の年間の消費量を計算する

まず、年間電力量E_需要について考えると、最大電力が100[MW]で年負荷率が60[%]、1年の総時間が8760[h]なので、設問(a)の(1)式と同じように考えると次のように計算できます。

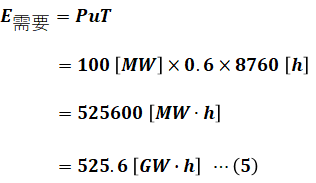
上記の(5)式と設問(a)の(4)式から、汽力発電で供給する年間発電量E_汽力は以下の(6)式のようになります。

続いて、汽力発電の入力で必要な熱エネルギーE_入力について考えます。すでに(6)式で汽力発電の発電量E_汽力がわかっていて、問題文より発電端効率η＝0.4と与えられているので、次のように計算することでE_入力を算出することができます。

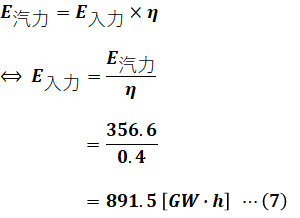
ただし、(7)式だと単位が[GW・h]となっていて、これは熱エネルギーの単位というより電力量の単位といえます。問題文の条件でまだ使っていない(これから使う)重油の発熱量の単位[kJ/L]のことを考えると、(7)式を[W]表記から[J]表記に変換しておく必要があります。

1[W・s]が1[J]なので、1[W・h]は3600[J]です。よって、(7)式の単位を変換すると、次の(8)式のように表すことができます。

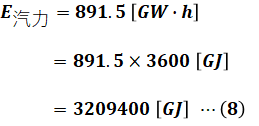
以上で汽力発電の入力で必要な熱エネルギーがわかりました。最後に、(8)式と重油の発熱量から、重油の年間の消費量を計算します。

よって、正解は(3)となります。