電験三種 R5年度上期 理論 問15 問題と解説

　問 題　　　　　

図の平衡三相回路について、次の(a)及び(b)の問に答えよ。

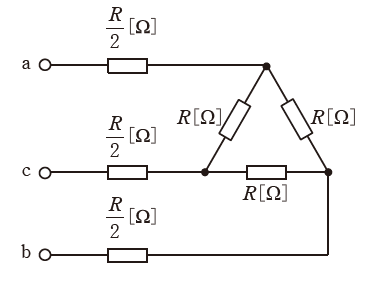
(a)　端子a、cに100Vの単相交流電源を接続したところ、回路の消費電力は200Wであった。抵抗Rの値[Ω]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 0.30
2. 30
3. 33
4. 50
5. 83

(b)　端子a、b、cに線間電圧200Vの対称三相交流電源を接続したときの全消費電力の値[kW]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 0.48
2. 0.80
3. 1.2
4. 1.6
5. 4.0

 

 

 

 

 

　解 説　　　　

(a)

設問(a)では端子a－c間に単相交流電源を接続しているので、端子bは関係ありません。つまり、問題の図は次のような図に描き換えることができます。

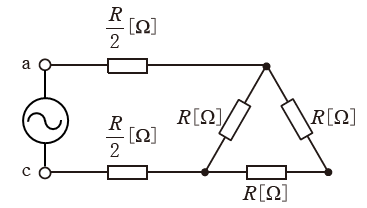
上図のままで考えても構いませんが、もう少し見やすくするため、さらに下図のように表します。

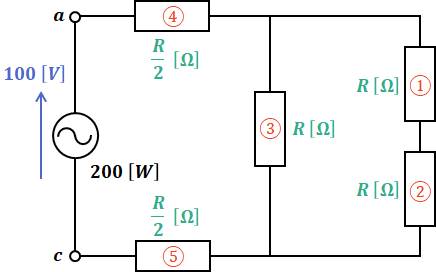
上図の①と②の抵抗が直列に並んでいるため、その合成抵抗R_1~2は次の(1)式で表されます。

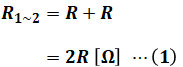
また、抵抗R_1~2と③の抵抗は並列接続なので、その合成抵抗R_1~3は次の(2)式で表されます。

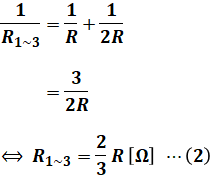
さらに、抵抗R_1~3と④と⑤の抵抗は直列接続となるので、その合成抵抗R_1~5は次の(3)式で表されます。

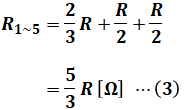
以上から、上図の回路は下図のように描き換えることができます。

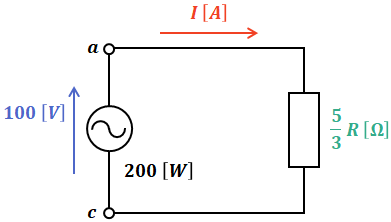
ここで、この回路の消費電力Pは200[W]と与えられているので、回路を流れる電流Iは次の(4)式のようになります。

よって、オームの法則より、抵抗Rの値は以下の(5)式のように計算することができます。

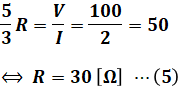
以上から、正解は(2)となります。

(b)

問題の回路は三相回路になっていて、このままでは考えにくいので、まずは三相回路から1相分の等価回路を抜き出して考えます。この際、Δ結線では中性点がなく等価回路が描けないので、Δ結線をY結線に直した上で下図のように等価回路を描きます。

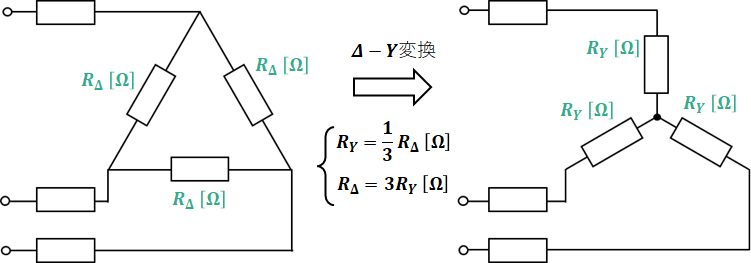
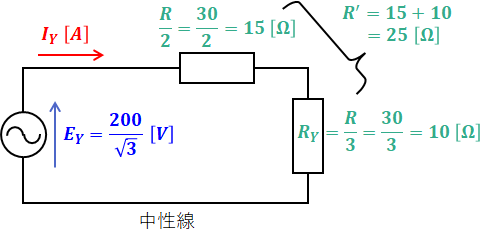
上図に示した通り、Δ－Y変換では1相あたりの抵抗の値は1/3倍となります。ただし、Δ－Y変換に関係ない線上の抵抗の値はそのままです。また、Y結線の相電圧E_Yは線間電圧E(＝Δ結線の相電圧E_Δ)の1/√3倍になります。

よって、この等価回路を流れる電流I_Yは次の(6)式のようになります。

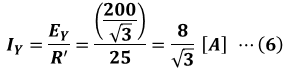
以上から1相分の等価回路の電流と電圧がわかったので、この等価回路の消費電力P[W]を計算することができます。ただし、これは1相分の消費電力Pであり、問われているのは三相回路の全消費電力です。つまり、Pを3倍した3P[W]が最終的な答えとなります。

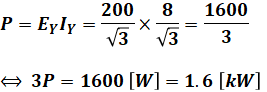
よって、正解は(4)です。