問 題
次の文章は、図1及び図2に示す原理図を用いてホール素子の動作原理について述べたものである。
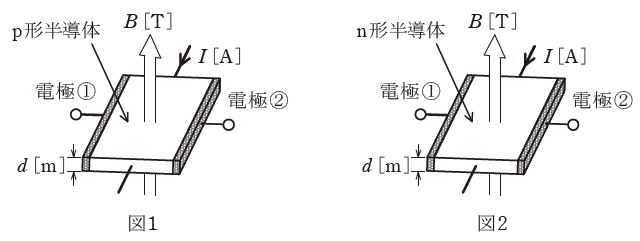
図1に示すように、p形半導体に直流電流I[A]を流し、半導体の表面に対して垂直に下から上向きに磁束密度B[T]の平等磁界を半導体にかけると、半導体内の正孔は進路を曲げられ、電極①には( ア )電荷、電極②には( イ )電荷が分布し、半導体の内部に電界が生じる。
また、図2のn形半導体の場合は、電界の方向はp形半導体の方向と( ウ )である。この電界により、電極①-②間にホール電圧VH=RH×( エ )[V]が発生する。
ただし、d[m]は半導体の厚さを示し、RHは比例定数[m3/C]である。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
- (ア) (イ) (ウ) (エ)
- 負 正 同じ B/Id
- 負 正 同じ Id/B
- 正 負 同じ d/BI
- 負 正 反対 BI/d
- 正 負 反対 BI/d
解 説
図1はp形半導体なので、キャリアは正孔(正電荷)となります。この正孔がどう動くのかというのは、電流と磁界の向きからフレミングの左手の法則を使って、電磁力の向きを考えるとわかります。
ここで、フレミングの左手の法則とは、左手の親指と人差し指と中指を互いに直交させたとき、指の向きと電流I、磁界B、電磁力Fとが以下のように対応するという法則です。
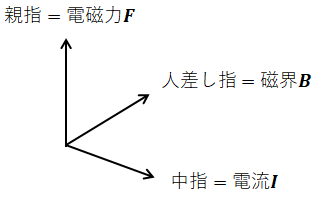
- 中指:電流Iの向き
- 人差し指:磁界Bの向き
- 親指:電磁力Fの向き
本問では、磁界Bが画面下から上へ、電流Iが画面奥から手前に向いているため、電磁力Fは画面右から左方向となります。つまり、正孔は電極①のほうに集まるため、電力①には正電荷、電極②には負電荷が分布することがわかります。
よって、( ア )には「正」、( イ )には「負」が入ると判断することができます。
続いて、図2はn形半導体なので、キャリアは電子(負電荷)となります。この電子の動き方は図1と同様で、フレミングの左手の法則に従います。つまり、電磁力が右から左に働き、電子は電極①に集まります。
ここで、図1のときには電極①に正電荷が分布した一方で、図2では電極①に負電荷が分布することになるため、生じる電界の方向は図1と図2では反対方向となります。
よって、( ウ )には「反対」が入ります。
残る( エ )についてはやや難易度が高いように感じますが、( ア )~( ウ )を答えられれば選択肢は1つに絞られるため、そこまでこだわらなくてもいいかもしれません。
ホール電圧VHの大きさは、以下の式で表すことができます。
![]()
- VH:ホール電圧 [V]
- RH:比例定数 [m3/C]
- B:磁束密度 [T]
- I:電流 [A]
- d:半導体の厚さ [m]
よって、( エ )には「BI/d」が入ります。
ただし、上式を知らない場合でも、本問では比例定数RHの単位が与えられているため、選択肢に出てくる変数の単位から正解を判断することもできます。
具体的には、磁束密度Bの単位[T]は[Wb/m2]であり、さらに[Wb]は[V・s]です。また、1[A]の電流が1秒間(1[s])流れたときの電気量が1[C]なので、[A]は[C/s]となります。すると、(1)式を単位で書き直すと次のようになります。
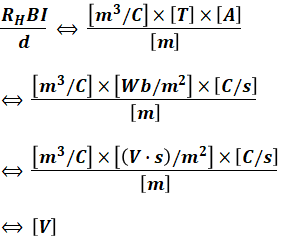
よって、( エ )は「BI/d」とするのが正しく、「B/Id」や「Id/B」、「d/BI」では成立しないことがわかります。
以上から、
- 正
- 負
- 反対
- BI/d
となるので、正解は(5)です。

コメント