問 題
静電界に関する次の記述のうち、誤っているものを次の(1)~(5)のうちから一つ選べ。
- 媒質中に置かれた正電荷から出る電気力線の本数は、その電荷の大きさに比例し、媒質の誘電率に反比例する。
- 電界中における電気力線は、相互に交差しない。
- 電界中における電気力線は、等電位面と直交する。
- 電界中のある点の電気力線の密度は、その点における電界の強さ(大きさ)を表す。
- 電界中に置かれた導体内部の電界の強さ(大きさ)は、その導体表面の電界の強さ(大きさ)に等しい。
解 説
(1)は正しいです。まず、電界の状態を仮想的な線で表したものを電気力線といいます。
そして、この電気力線は無数に放射されていて数えきれないので、1[C]分の電気力線のまとまりを「電束」と呼びます。1[C]の電荷からは1束の電束が放射される、というイメージです。よって、電気力線の本数はその電荷の大きさに比例します。
また、問1の解説でも紹介した通り、電束密度D[C/m2]は誘電率ε[F/m]と電界の強さE[V/m]の積で表すことができます。これを以下のように式を変形することで、電界の強さEは誘電率εに反比例することがわかります。すると、電気力線は電界の状態を表すものなので、電気力線も誘電率に反比例するといえます。
![]()
(2)も正しいです。電気の+と-(正電荷と負電荷)は、磁石のNとSのような関係にあります。たとえば、電気における電気力線は、磁石における磁力線に対応します。方位磁針の磁力線は下図のような感じですが、同様に、正電荷と負電荷が作る電気力線は、さらに下の図のようになります。
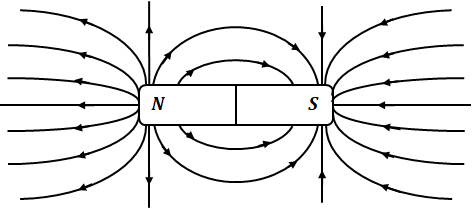
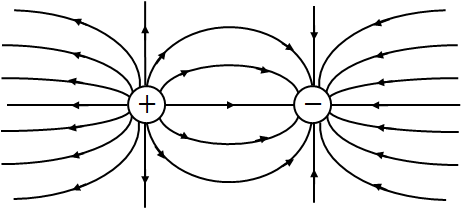
上図からわかるように、電気力線は途中で分岐したり、他の電気力線と交差したりしません。
もし仮に電気力線が交差するとすると、その交点において電界の向きが二つ以上存在することになります。しかし、電界の向きはその点に置かれた微小な正電荷に働く力の向きと一致するので、必ず一つの向きを示します。よって、電気力線が交差することは有り得ません。
(3)も正しいです。等電位面とは、その面上の全ての点で電位が等しい面のことです。電位差は、電界と平行に移動した距離に比例するので、等電位面に沿って移動すると電位差は0になります。よって、電界は常に等電位面と垂直の関係となります。
(4)も正しいです。電気力線の密度とは、単位面積あたりの電気力線の本数のことです。(1)でも解説した通り、電気力線の本数は電界の強さに比例するので、電気力線の密度も電界の強さに比例します。
(5)が誤りです。電界中に置かれた導体内部の電界の強さは、常に0[V/m]となります。これは、導体内部を自由に動くことができる電荷が、電界によって導体表面に移動し、内部の電界を打ち消すためです。
つまり、(5)の後半にある「その導体表面の電界の強さ(大きさ)に等しい。」が誤りで、これを「0となる。」などに直せば、正しい文章となります。
以上から、正解は(5)です。

コメント