電験三種 R5年度上期 機械 問17 問題と解説

　問 題　　　　　

熱伝導について、次の(a)及び(b)の問に答えよ。断面積が2m²、厚さが30cm、熱伝導率が1.6W/(m・K)の両表面間に温度差がある壁がある。ただし、熱流は厚さ方向のみの一次元とする。

(a)　この壁の厚さ方向の熱抵抗Rの値[K/W]に最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 0.0417
2. 0.0938
3. 0.267
4. 2.67
5. 4.17

(b)　この壁の低温側の温度t₂が20℃のとき、この壁の熱流Φが100Wであった。このとき、この壁の高温側の温度t₁の値[℃]に最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 21.0
2. 22.1
3. 24.2
4. 29.4
5. 46.7

 

 

 

 

 

　解 説　　　　

(a)

熱抵抗R[K/W]は熱の通しにくさを表すパラメータで、その単位からもわかるように、温度差θ[K]を熱流Φ[W]で割った値となります。

• R：熱抵抗 [K/W]
• θ：温度差 [K]
• Φ：熱流 [W]

とはいえ、今回は問題文で与えられているのが温度差θや熱流Φではなく、断面積S[m²]、厚さd[cm]、熱伝導率λ[W/(m・K)]となっています。これらと熱抵抗Rとの関係式を無理に覚えておく必要はないと思いますが、単位に注目しながら考えると、次の(2)式の関係式が成り立つことがわかります。

よって、問題文で与えられている各数値を(2)式に代入すると、熱抵抗Rを算出することができます。ただし、厚さdの単位は[cm]として与えられているので、計算をする際には[m]に直すのを忘れないでください。

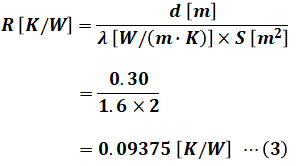
以上から、正解は(2)となります。

(b)

設問(b)で問われているのは壁の高温側の温度t₁であり、与えられているパラメータに熱流Φがあります。つまり、設問(a)の解説の冒頭で紹介した(1)式を使うことになるので、以下に再度示します。

• R：熱抵抗 [K/W]
• θ：温度差 [K]
• Φ：熱流 [W]

(1)式において、熱抵抗Rは設問(a)の(3)式で求めてあり、熱流Φは問題文に記載があるため、温度差θは次のように求めることができます。

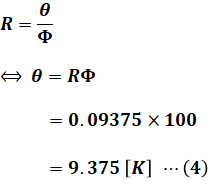
ここでいう温度差というのは、壁の両表面間の温度差です。また、温度差の単位は[K](ケルビン)となっていますが、これは[℃]に置き換えることができます。Kは絶対温度、℃は摂氏として使われますが、「温度差」として用いる限りは両者を区別する必要はありません。

よって、温度差が(4)式のように9.375[K]であれば、これは9.375[℃]と表すこともできます。そのため、低温側の温度t₂が20[℃]であれば、高温側の温度t₁[℃]の値は次のようになります。

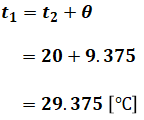
以上から、正解は(4)となります。