電験三種 R5年度上期 機械 問6 問題と解説

　問 題　　　　　

次のような三相同期発電機がある。

• 1極当たりの磁束：0.10Wb
• 極数　　　　　  ：12
• 1分間の回転速度：600min^－1
• 1相の直列巻数　：250
• 巻線係数　　　  ：0.95
• 結線　　　　　  ：Y(1相のコイルは全部直列)

この発電機の無負荷誘導起電力(線間値)の値[kV]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、エアギャップにおける磁束分布は正弦波であるものとする。

1. 2.09
2. 3.65
3. 6.33
4. 11.0
5. 19.0

 

 

 

 

 

　解 説　　　　

問われているのは「三相同期発電機の無負荷誘導起電力(線間値)の値」ですが、三相同期発電機の誘導起電力といえば、まずは内部誘導起電力の式を思い出してほしいところです。

三相同期発電機の一相あたりの内部誘導起電力(相電圧実効値)は、以下の式で表すことができます。なお、内部誘導起電力とは、同期電動機の電機子端子電圧(相電圧実効値)から電機子電流の影響を除いた電圧です。

• E：内部誘導起電力 [V] (1相あたりの相電圧実効値)
• k_w：巻線係数
• f：周波数 [Hz]
• Φ：磁束 [Wb] (1極あたり)
• N：巻数 (1相あたり)

ただし、求めたい無負荷誘導起電力(線間値)Vと上記の内部誘導起電力(相電圧実効値)Eを比較すると、Vは問題文よりY結線の線間電圧であり、Eは(1)式より相電圧であることがわかります。つまり、VとEには次のような関係があります。

• V：無負荷誘導起電力(線間値) [V]
• E：内部誘導起電力(相電圧実効値) [V]

よって、(1)式の値を求めることができれば、それを(2)式に代入することによって答えが得られます。

なお、(1)式の右辺に出てくる各変数のうち、巻線係数k_w、磁束Φ、巻数Nの値はすでに問題文で与えられています。一方で周波数fは未知数なので、以下の(3)式で示される同期速度の式を使って(4)式のように算出します。

• N_s：同期速度 [min^-1]
• p：磁極の数 [極]
• f：周波数 [Hz]

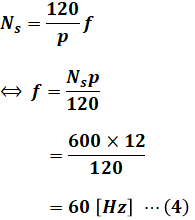
よって、(4)式を(1)式に代入し、さらに(2)式に代入することで、求めたい無負荷誘導起電力(線間値)Vを算出することができます。

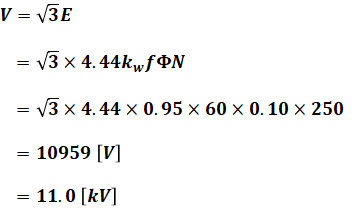
以上から、正解は(4)となります。