電験三種 R5年度上期 電力 問12 問題と解説

　問 題　　　　　

こう長2kmの三相3線式配電線路が、遅れ力率85%の平衡三相負荷に電力を供給している。負荷の端子電圧を6.6kVに保ったまま、線路の電圧降下率が5.0%を超えないようにするための負荷電力[kW]の最大値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、1km1線当たりの抵抗は0.45Ω、リアクタンスは0.25Ωとし、その他の条件は無いものとする。なお、本問では送電端電圧と受電端電圧との相差角が小さいとして得られる近似式を用いて解答すること。

1. 1023
2. 1799
3. 2117
4. 3117
5. 3600

 

 

 

 

 

　解 説　　　　

線路の電圧降下は次の式で表すことができます。これは公式として覚えておきたい知識ですが、導出過程が気になる方は三相3線式送電線の電圧降下のページを参照してください。

• V_d：電圧降下 [V]
• V_s：送電端電圧 [V]
• V_r：受電端電圧 [V]
• I：線電流 [A]
• R：抵抗 (電線1条あたり) [Ω]
• X：リアクタンス (電線1条あたり) [Ω]
• cosθ：負荷の力率

問題文に「近似式を用いて解答すること」とあるので、上式の左辺と右辺を使います(真ん中は使いません)。上式に問題文で与えられた数値を代入していきたいのですが、直接入れられないものが多いので注意してください。

まず、V_dは電圧降下ですが、これは6.6[kV]の5.0[%]なので、6600×0.05＝330[V]となります。また、抵抗とリアクタンスは1kmあたりの数値がわかっていますが、今回はこう長2kmなので、2倍にします。つまり、R=0.9[Ω]、X=0.5[Ω]です。

よって、上に示した公式は以下のようになり、線電流Iを計算することができます。

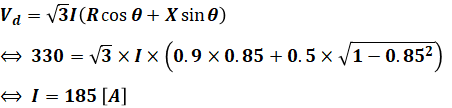
これでV、I、cosθの数値が全てわかったので、負荷電力Pを次のように計算することができます(答えの選択肢と微妙にずれてしまっているは、途中式の端数処理を何桁まで行うかの違いによるものです)。

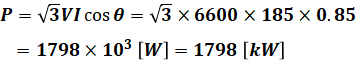
以上から、正解は(2)となります。