問 題
図1の回路は、電流帰還バイアス回路に結合容量を介して、微小な振幅の交流電圧を加えている。この入力電圧の振幅がAi=100mV、角周波数がω=10000rad/sで、時刻t[s]に対してvi(t)[mV]がvi(t)=Aisinωtと表されるとき、次の(a)及び(b)の問に答えよ。
(a) 次の文章は、電圧vB(t)に関する記述である。
トランジスタのベース端子に流れ込む電流iB(t)が十分に小さいとき、ベース端子を切り離しても2kΩの抵抗の電圧は変化しない。そこで、図2の回路で考え、さらに重ね合わせの理を用いることで、電圧vB(t)を求める。
まず、vi(t)=0Vとすることで、直流電圧VB=( ア )Vが求められる。
次に、直流電圧源の値を0Vとし、コンデンサのインピーダンスが2kΩより十分に小さいと考えると、交流電圧vB(t)の振幅AB=( イ )mVと初期位相θB=( ウ )radが求められる。
以上より、vB(t)=VB+ABsin(ωt+θB)と表すことができる。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
- (ア) (イ) (ウ)
- 0.8 71 0
- 0.8 100 π/4
- 1.5 71 π/4
- 1.5 100 0
- 1.5 71 0
(b) 図1の回路の電圧vC(t)を求め、適当な定数VC、AC、θCを用いてvC(t)=VC+ACsin(ωt+θC)と表す。VC、AC、θCに最も近い値の組合せを次の(1)~(5)のうちから一つ選べ。
ただし、ベース・エミッタ間電圧は常に0.7Vであると近似して考えてよい。
- VC[V] AC[V] θC[rad]
- 5 0.6 0
- 5 6 0
- 5 6 π
- 7 0.6 π
- 7 6 π
解 説
(a)
本問では、重ね合わせの理を用いて2[kΩ]の抵抗の端子間電圧vB(t)を求めることが示されています。
つまり、まずは交流電源がないもの(短絡状態)として扱い、vB(t)のうち直流電源由来のVBを考えます。そして次に、直流電源がないもの(短絡状態)として扱い、vB(t)のうち交流電源由来のABsin(ωt+θB)について考えます。
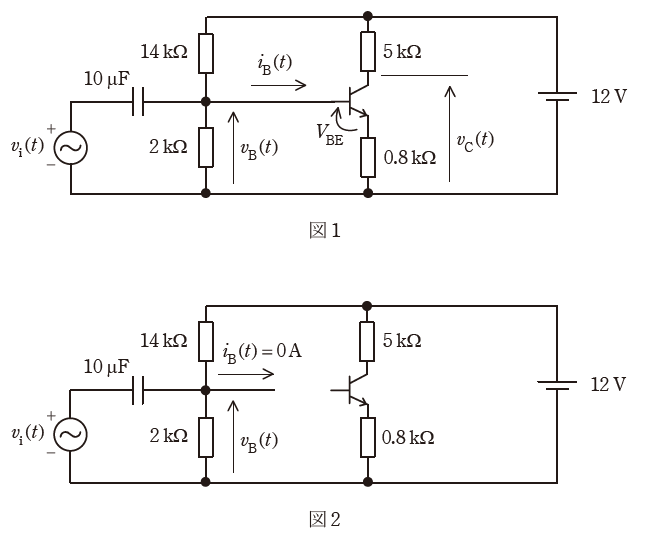
ここで、交流電源がないもの(vi(t)=0V)とすると、図2は以下のように描き換えることができます。
上図の赤矢印で示した回路で考えると、14[kΩ]と2[kΩ]の2つの抵抗を合わせた端子間電圧が12[V]となるので、2[kΩ]の抵抗の端子間電圧VB[V]は次のように計算することができます。
![]()
よって、( ア )には「1.5」が入ります。
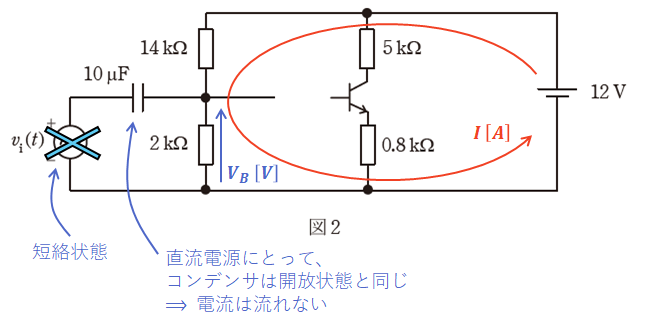
続いて、直流電源がないもの(短絡状態)として考えます。また、問題文よりコンデンサのインピーダンスも0[Ω]と考えてよいので、コンデンサも短絡していると見なすことができます。よって、図2は以下のように描き換えることができます。
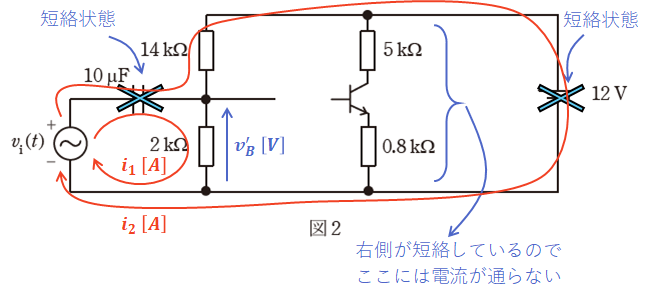
上図の2つの赤矢印を交流電源からたどっていくと、電源から出た電流が途中で分岐し、再度合流して電源に戻っています。つまり、上図は以下のような並列回路であることがわかります。
ここで、( イ )と( ウ )で問われているのはvB(t)の交流電源由来である「v’B(t)=ABsin(ωt+θB)」のうち、「AB」と「θB」の値です。
上図より、この回路はコイルもコンデンサもなく、単純に2つの抵抗が並列に並んだ回路であるので、v’B(t)は入力電圧「vi(t)=Aisinωt」と全く同一であることがわかります。よって、問題文より「Ai=100[mV]」なので、「AB=100[mV]」かつ「θB=0」となります。
よって、( イ )には「100」が、( ウ )には「0」が入ります。
最後に重ね合わせの理を使ってまとめると、2[kΩ]の抵抗の端子間電圧vB(t)は次のように表すことができます。
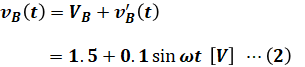
以上から、( ア )は「1.5」、( イ )は「100」、( ウ )は「0」となるので、正解は(4)です。
(b)
まず、図1を改めて以下に示します。
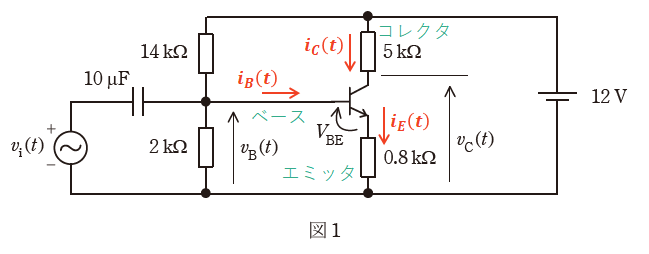
問われているのはvC(t)の式の詳細であるため、まずはvC(t)を表す式を組み立てることを考えます。上図右側部分の直流電源と5[kΩ]、0.8[kΩ]の抵抗を含む四角形より、vC(t)の式は以下のように書くことができます。
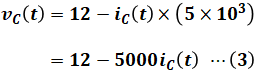
ここで、今回のようなエミッタ接地増幅回路の場合、電圧増幅率や電流増幅率が大きく、ベース電流iB(t)はコレクタ電流iC(t)やエミッタ電流iE(t)に比べて極端に小さくなります。そのため、設問(a)ではiB(t)=0[A]と見なしています。
本来なら上図の通りiB(t)とiC(t)の和がiE(t)になりますが、iC(t)やiE(t)と比べてiB(t)はかなり小さいので、計算上は「iC(t)=iE(t)」と近似することができます。つまり、(3)式は以下の(4)式のように書き換えることができます。
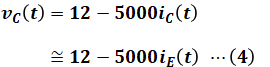
(3)式のままではiC(t)を表す式の見当がつきませんでしたが、(4)式ではiE(t)を使う式になったので、上図のベースとエミッタを含む小さな四角形より、次の等式が成り立ちます。

さらに、(5)式を(4)式に代入すると、次の(6)式のようになります。

ここで、VBEは問題文より0.7[V]であり、vBは設問(a)の(2)式で求めています。よって、これらを(6)式に代入して計算を進めれば、vC(t)の式を立てることができます。
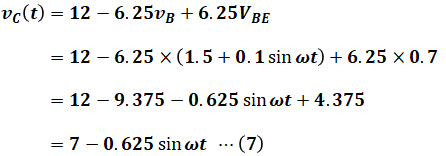
これでほぼ答えが出ていますが、最後に注意すべき点があります。(7)式ではsinを含む項の符号がマイナスになっていますが、これでは問題文に書かれている「vC(t)=VC+ACsin(ωt+θC)」の形と合っていません。
よって、最後にこのマイナスをプラスに変える必要があります。そして符号を変えるということは位相がπ(180°)ずれるということ(-sinθ=sin(θ+π))なので、(7)式は以下の(8)式のように変換できます。

以上から、(8)式と「vC(t)=VC+ACsin(ωt+θC)」を比較すると、「VC=7」、「AC=0.6」(0.625を四捨五入)、「θC=π」であることがわかります。
よって、正解は選択肢(4)となります。

コメント