電験三種 R4年度下期 理論 問17 問題と解説

　問 題　　　　　

大きさが等しい二つの導体球A、Bがある。両導体球に電荷が蓄えられている場合、両導体球の間に働く力は、導体球に蓄えられている電荷の積に比例し、導体球間の距離の2乗に反比例する。次の(a)及び(b)の問に答えよ。

ただし、両導体球の大きさは0.3mに比べて極めて小さいものとする。

(a)　この場合の比例定数を求める目的で、導体球Aに＋2×10^－8C、導体球Bに＋3×10^－8Cの電荷を与えて、導体球の中心間距離で0.3m隔てて両導体球を置いたところ、両導体球間に6×10^－5Nの反発力が働いた。

この結果から求められる比例定数[N・m²/C²]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、導体球A、Bの初期電荷は零とする。

1. 3×10⁹
2. 6×10⁹
3. 8×10⁹
4. 9×10⁹
5. 15×10⁹

(b)　小問(a)の導体球A、Bを、電荷を保持したままで0.3mの距離を隔てて固定した。ここで、導体球A、Bと大きさが等しく電荷を持たない導体球Cを用意し、導体球Cをまず導体球Aに接触させ、次に導体球Bに接触させた。

この導体球Cを図のように導体球Aと導体球Bの間の直線上に置くとき、導体球Cが受ける力が釣り合う位置を導体球Aとの中心間距離[m]で表したとき、その距離に最も近いものを次の(1)～(5)のうちから一つ選べ。

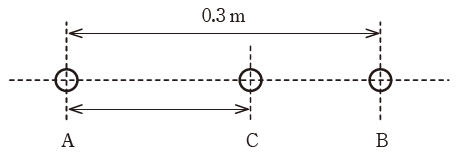
1. 0.095
2. 0.105
3. 0.115
4. 0.124
5. 0.135

 

 

 

 

 

　解 説　　　　

(a)

問題文の前半に書かれている通り、両導体球の間に働く力は、導体球に蓄えられている電荷の積に比例し、導体球間の距離の2乗に反比例します。このことを式にすると、次のように書くことができます。

• F：静電気力 [N]
• K：比例定数 [N・m²/C²]
• Q_A、Q_B：導体球A、Bの電荷 [C]
• r：電荷間の距離 [m]

(1)式に問題文で与えられた各数値を代入してKについて解けば、問われているKの値を求めることができます。

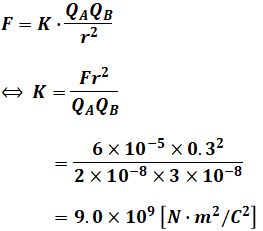
よって、正解は(4)となります。

(b)

まず、接触前の導体球A、B、Cの電荷は、それぞれQ_A＝＋2×10^－8[C]、Q_B＝＋3×10^－8[C]、Q_C＝0[C]です。

ここで、2つの導体球を接触させると、電荷が高いほうから低いほうへと流れ、2つの導体球の電荷は等しくなります。よって、導体球AとCを接触させると、Q_AとQ_Cは以下に示すように2つの平均値であるQ’_A＝Q’_Cへと変化します。

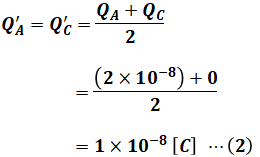
続いて、導体球BとCを接触させると、Q_BとQ’_Cは以下に示すように2つの平均値であるQ’_B＝Q”_Cへと変化します。

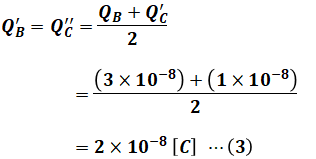
以上のことを問題の図に描き込むと、次のように表すことができます。

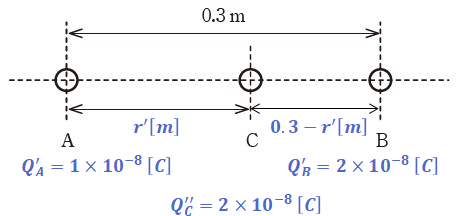
上図において、導体球Cが受ける力が釣り合っているなら、AC間に働く静電気力とBC間に働く静電気力は同一の値となっているはずです。

そのため、(1)式を使って2つの静電気力をイコールで結び、(2)式と(3)式を用いてr’について解けば、AC間の距離を求めることができます。

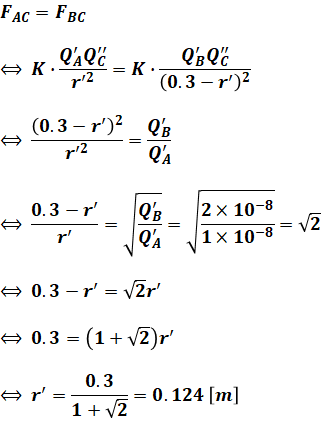
以上から、正解は(4)となります。