電験三種 R4年度下期 理論 問15 問題と解説

　問 題　　　　　

図のように、抵抗6Ωと誘導性リアクタンス8ΩをY結線し、抵抗r[Ω]を結線した平衡三相負荷に、200Vの対称三相交流電源を接続した回路がある。抵抗6Ωと誘導性リアクタンス8Ωに流れる電流の大きさをI₁[A]、抵抗r[Ω]に流れる電流の大きさをI₂[A]とする。

電流I₁[A]とI₂[A]の大きさが等しいとき、次の(a)及び(b)の問に答えよ。

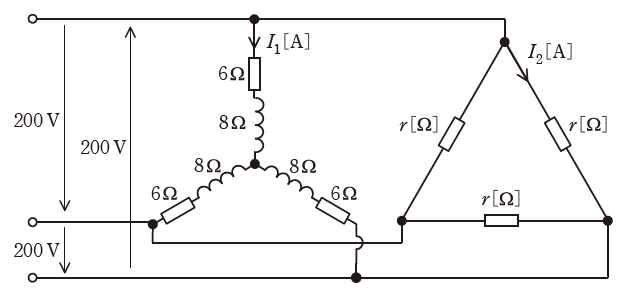
(a)　抵抗rの値[Ω]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 6.0
2. 10.0
3. 11.5
4. 17.3
5. 19.2

(b)　図中の回路が消費する電力の値[kW]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 2.4
2. 3.1
3. 4.0
4. 9.3
5. 10.9

 

 

 

 

 

　解 説　　　　

(a)

電流I₁が流れるY結線のほうに注目すると、電圧もインピーダンスも既知の値であるため、これは計算によって電流I₁を算出することができそうです。

一方、電流I₂が流れるΔ結線のほうは、電圧が既知で電流と抵抗が未知です。しかし、問題文よりI₁＝I₂なので、先にY結線を使ってI₁を求めてから、次にΔ結線を使って抵抗rを求めるというのが解法の流れとなります。

そこで、まずはY結線のほうの1相分の等価回路について考えると、次のような回路を描くことができます。なお、Y結線の場合は等価回路に仮想中性線を用いるため、等価回路の電源電圧は線間電圧の√3分の1倍になります。

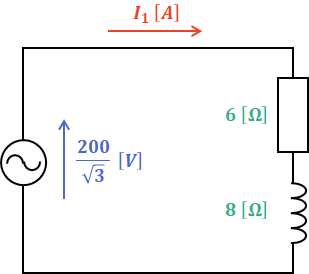
上図より、電流I₁は次のように算出できます。

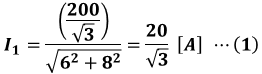
続いて、Δ結線のほうの1相分の等価回路について考えると、次のような回路を描くことができます。今度の場合は、抵抗rの端子間電圧と線間電圧が一致するので、等価回路の電源電圧も線間電圧の値となります。

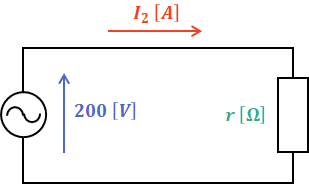
ここで、I₁＝I₂より、抵抗rは(1)式を使って次のように計算することができます。

よって、正解は(4)となります。

(b)

設問(a)でI₁、I₂、rの値がすでにわかっているので、各抵抗で消費する電力をそれぞれ計算し、それらを合計したものが答えとなります。

なお、問われているのは消費電力の値[kW]なので、有効電力ではない(＝無効電力である)8[Ω]の誘導性リアクタンスについては考える必要がありません。

そこで、まずは6[Ω]の抵抗1つ分が消費する電力P₍₆₎[kW]を計算すると、次のようになります。

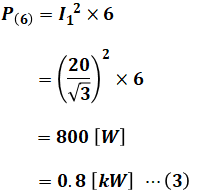
続いて、r[Ω]の抵抗1つ分が消費する電力P_(r)[kW]を計算すると、次のようになります。

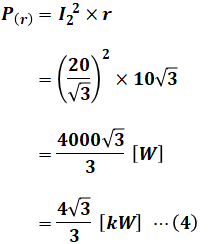
よって、この回路には6[Ω]の抵抗3つ分とr[Ω]の抵抗3つ分があるため、回路全体での消費電力P[kW]の値は、(3)式と(4)式を使って次のように計算することができます。

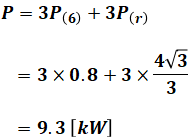
以上から、正解は(4)となります。