電験三種 R4年度下期 理論 問5 問題と解説

　問 題　　　　　

図のような直流回路において、抵抗3の端子間の電圧が1.8Vであった。このとき、電源電圧E[V]の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

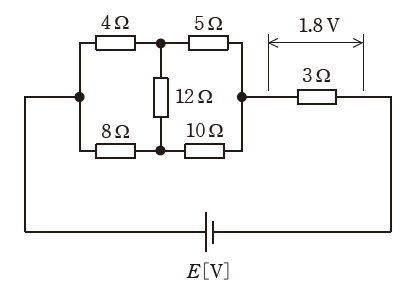
1. 1.8
2. 3.6
3. 5.4
4. 7.2
5. 10.4

 

 

 

 

 

　解 説　　　　

本問のように、四角形の辺上にある4つの抵抗に加え、その中心にもう1つの抵抗が並んでいる場合、まずブリッジ回路である可能性を考えたいです。

ブリッジ回路において、四角形の辺上に位置する4つの抵抗のうち、向かい合う2組の抵抗の積が等しいとき、このブリッジ回路は「平衡状態にある」と表現されます。平衡状態にあるときには、四角形の中央にある抵抗には一切電流が流れません。

今回の場合、四角形の辺上に位置する4つの抵抗について、向かい合う2組の抵抗の積はいずれも40で等しいです。よって、中央にある12[Ω]の抵抗には電流が流れません。

つまり、この中央の12[Ω]の抵抗は無いものと見なすことができるので、問題の図は下図のように描き換えることができます。

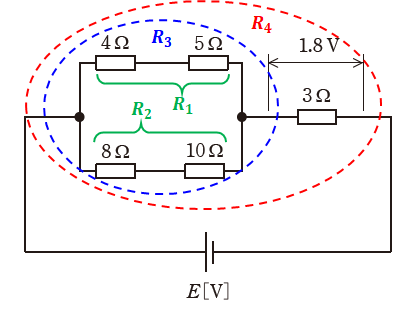
上図から、この回路の合成抵抗を求めるには、次のように整理しながら計算していけばよいことになります。

1. R₁：4[Ω]と5[Ω]の直列接続
2. R₂：8[Ω]と10[Ω]の直列接続
3. R₃：上記R₁とR₂の並列接続
4. R₄：上記R₃と3[Ω]の直列接続

よって、回路全体の合成抵抗は次のように計算することができます。

ここで、電源を流れる電流Iの大きさは、問題文にある抵抗3[Ω]の端子間電圧1.8[V]から求めることができます。

以上から、(1)式と(2)式より、電源電圧E[V]は次のようになります。

よって、正解は(3)です。