電験三種 R4年度下期 理論 問3 問題と解説

　問 題　　　　　

無限に長い直線状導体に直流電流を流すと、導体の周りに磁界が生じる。この磁界中に小磁針を置くと、小磁針の(　ア　)は磁界の向きを指して静止する。

そこで、小磁針を磁界の向きに沿って少しずつ動かしていくと、導体を中心とした(　イ　)の線が得られる。この線に沿って磁界の向きに矢印をつけたものを(　ウ　)という。

また、磁界の強さを調べてみると、電流の大きさに比例し、導体からの(　エ　)に反比例している。

上記の記述中の空白箇所(ア)～(エ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

• (ア)　　　(イ)　　　　(ウ)　　　　(エ)

1. N極　　放射状　　　電気力線　　距離の2乗
2. N極　　同心円状　　電気力線　　距離の2乗
3. S極　　放射状　　　磁力線　　　距離
4. N極　　同心円状　　磁力線　　　距離
5. S極　　同心円状　　磁力線　　　距離の2乗

 

 

 

 

 

　解 説　　　　

無限に長い直線状導体に直流電流を流すと、下図のようにその電流に応じた強さの磁界が導体の周りに円を描くように発生します。

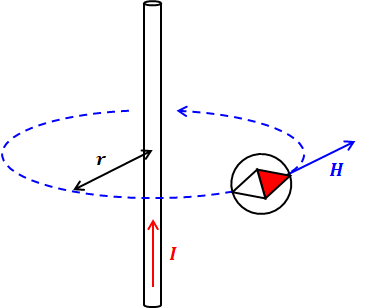
このとき、直線導体を流れる電流がつくる磁界Hは、以下の式で表されます。今回は計算問題ではありませんが、この式は重要公式としてぜひ押さえておきたい知識です。

• H：磁界 [A/m]
• I：電流 [A]
• r：導体と磁界の距離 [m]

また、磁界には向きがあります。上図の通り、電流が画面下から画面上に流れている場合、磁界の向きは(上から見て)反時計回りとなります。これは、右ねじの法則に従っています。

以上を踏まえて問題文を見ると、(　ア　)には「N極」、(　イ　)には「同心円状」が入ることがわかります。

(　ウ　)について、磁界の向きに矢印をつけたものは「磁力線」といいます。選択肢にある「電気力線」は、正電荷から負電荷へと向かう線のことです。電気力線の磁気バージョンが磁力線となります。

(　エ　)で、上で示した磁界Hの式を見るとわかるように、導体と磁界の距離rはHに反比例します。よって、(　エ　)は「距離」を選ぶのが適切です。

以上から、(　ア　)は「N極」、(　イ　)は「同心円状」、(　ウ　)は「磁力線」、(　エ　)は「距離」となるので、正解は(4)です。