電験三種 R4年度下期機械問16 問題と解説

　問題　　　　　

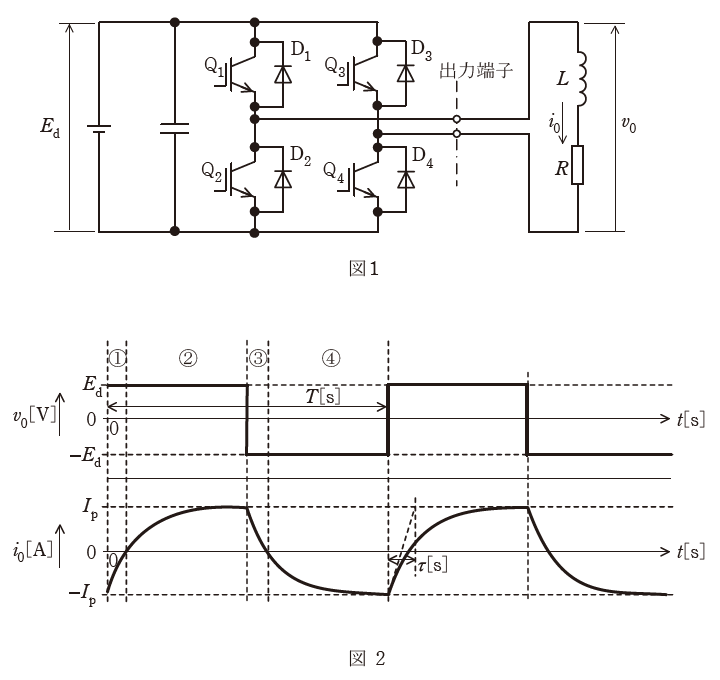
図1は、IGBTを用いた単相ブリッジ接続の電圧形インバータを示す。直流電圧E_d[V]は、一定値と見なせる。出力端子には、インダクタンスL[H]で抵抗値R[Ω]の誘導性負荷が接続されている。この電圧形インバータの出力電圧v₀、出力電流i₀が図2のようになった。

インバータの動作モードを図2に示す①～④として本モードは周期T[s]で繰り返されるものとする。なお、上下スイッチの短絡を防ぐデッドタイムは考慮しない。

次の(a)及び(b)の問に答えよ。

(a)　図2に示した区間①～④において電流が流れているデバイスの組合せとして正しいものを次の(1)～(5)のうちから一つ選べ。

(b)　電源電圧E_dが100V、インダクタンスLを2mHとし、抵抗Rを1Ωとすると、区間①②の電流は－I_p[A]からI_p[A]まで時定数τ[s]で増加する。τに最も近い値を次の(1)～(5)のうちから一つ選べ。

正解 (a)-(2), (b)-(2)

　解説　　　　

図2に示された区間①～④を確認すると、それぞれ次のようになっていることがわかります。

上記のそれぞれの区間の場合に電流がどの経路をたどるかについて、図1を使いながら以下で解説していきます。

【区間①】v₀＝＋E_d、i₀＜0

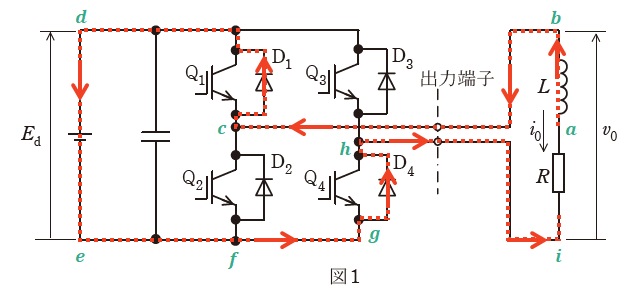
区間①の場合、電流は、上図赤線の経路を点aから点iまでアルファベット順に流れます(電流は回路内を回っているので、aが起点である必要はありません)。

考え方としては、まず区間①では「i₀＜0」より、点aを流れる電流の向きは図1に書き込んである「↓」向きとは逆の上向きだとわかります。そして、点bを経由して点cまで進みます。

点cで上下どちらに進むかが問題ですが、「v₀＝＋E_d」から、「v₀の上側である点b」と「E_dの上側である点d」が(電源を介さずに)同じ側に位置することがわかります。もしも点bと点eを(電源を介さずに)つなげてしまうと、v₀とE_dの正負が反対になってしまいます(v₀＝－E_d)。

よって、点cから向かうのは点dのある上側です。また、デバイスD₁を進むかQ₁を進むかについては、電流の進行方向と矢印の向きが合うほうとなるので、D₁を選ぶのが正しいです。

その後、点d、点e、点fと進みます。また、点fから上に進んでしまうと点aに戻る前に回路が閉じてしまうので、点fからは右側の点gへと進みます。そして、点gではデバイスD₄を通って点iへと至り、さらに点aまで進めば回路を1周したことになります。

以上から、区間①において電流の流れるデバイスは「D₁－D₄」となります。

【区間②】v₀＝＋E_d、i₀＞0

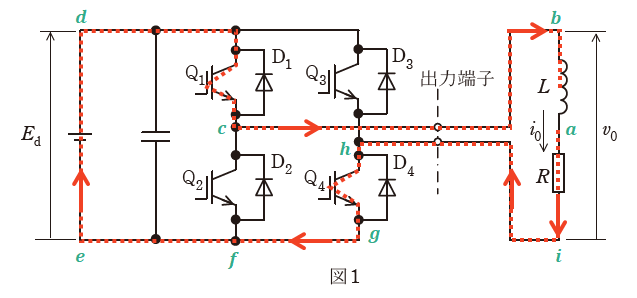
区間②の場合は「i₀＞0」なので、点aを流れる電流の向きが区間①のときとは逆向きになります。つまり、点a→点i→点hと進みます。

ここで、今回も「v₀＝＋E_d」なので、「v₀の下側である点i」と「E_dの下側である点e」が(電源を介さずに)同じ側に位置するので、点hから下方向の点gへと進みます。このときに通過するデバイスは、電流の進行方向と矢印の向きが合うQ₄です。

あとは区間①のときの同様に考えると、上図のような軌跡となるため、区間②において電流の流れるデバイスは「Q₁－Q₄」となります。

【区間③】v₀＝－E_d、i₀＞0

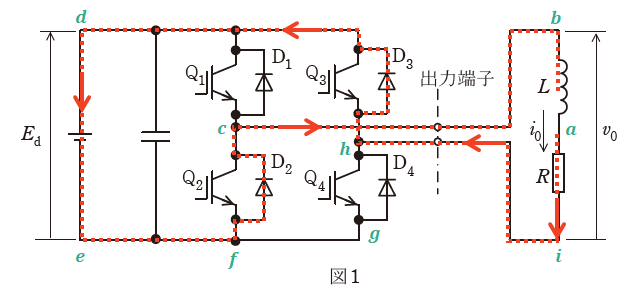
区間③では「i₀＞0」なので、点a→点iの方向となります。また、点hでの上下の分岐ですが、「v₀＝－E_d」から、「v₀の下側である点i」と「E_dの上側である点d」を接続する必要があります。そのため、点hから上へと進みます。

あとは区間①や区間②と同様に考えればよく、結果として、区間③において電流の流れるデバイスは「D₂－D₃」であることがわかります。

【区間④】v₀＝－E_d、i₀＜0

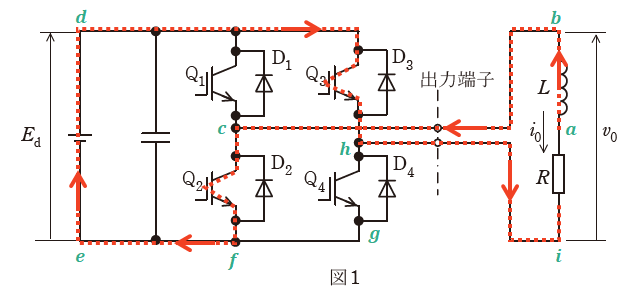
ここまでのことが理解できれば、区間④は説明不要だと思います。上図の通り、区間④において電流の流れるデバイスは「Q₂－Q₃」となります。

以上から、区間①は「D₁－D₄」、区間②は「Q₁－Q₄」、区間③は「D₂－D₃」、区間④は「Q₂－Q₃」となるので、正解は(2)です。

設問(b)では「時定数τ」が問われていますが、これは、電流や電圧(今回は電流)が立ち上がってから最大値(定常状態)の約63.2%になるまでに掛かった時間のことをいいます。

RL直列回路における時定数τの式は、以下のように表すことができます。

ちなみに、本問とは関係ありませんが、RC直列回路における時定数τの式は、以下のように表すことができます。

今回は図1の通りRL直列回路であるので、問題文で与えられているLとRの値を(1)式に代入して計算すれば、時定数τを算出することができます。

よって、正解は(2)となります。

コメント