電験三種 R4年度下期 機械 問11 問題と解説

　問 題　　　　　

電動機で駆動するポンプを用いて、毎時80m³の水をパイプへ通して揚程40mの高さに持ち上げる。ポンプの効率は72%、電動機の効率は93%で、パイプの損失水頭は0.4mであり、他の損失水頭は無視できるものとする。

このとき必要な電動機入力[kW]の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、水の密度は1.00×10³kg/m³、重力加速度は9.8m/s²とする。

1. 0.013
2. 0.787
3. 4.83
4. 13.1
5. 80.4

 

 

 

 

 

　解 説　　　　

まず、本問での揚程は40[m]ですが、パイプの損失水頭が0.4[m]あるので、実際には40.4[m]を揚げるだけのエネルギーが必要となります。

ここで、ポンプで揚水するというのは、電動機の出力を位置エネルギーに変えるということです。そのため、ポンプ出力P_oは位置エネルギーの公式を使って以下のように表されます。

• P_o：ポンプ出力 [kW]
• Q：流量 [m³/s]
• g：重力加速度 9.8[m/s²]
• H：全揚程 40.4[m]

これが揚水に必要なポンプ出力P_oです。しかし、実際には諸々の損失が生じるため、電動機入力P_inはもっと大きな値が必要です。具体的には、電動機入力P_inに電動機の効率η_mを掛けると電動機出力となり、これにさらにポンプの効率η_pを掛けたものがポンプ出力P_oとなるので、以下の等式が成り立ちます。

(1)式と(2)式より、問われている電動機入力P_inは次のように算出することができます。なお、水量Qの単位は[m³/s]なので、問題文の「毎時」を「毎秒」に変換するのを忘れないようにしてください。

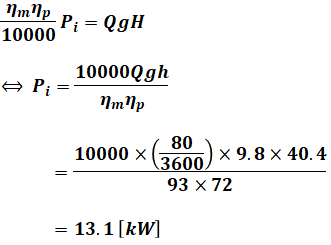
よって、正解は(4)となります。