電験三種 R4年度上期 理論 問17 問題と解説

　問 題　　　　　

図のように直列に接続された二つの平行平板コンデンサに120Vの電圧が加わっている。コンデンサC₁の金属板間は真空であり、コンデンサC₂の金属板間には比誘電率ε_rの誘電体が挿入されている。

コンデンサC₁、C₂の金属板間の距離は等しく、C₁の金属板の面積はC₂の2倍である。このとき、コンデンサC₁の両端の電圧が80Vであった。

次の(a)及び(b)の問に答えよ。

ただし、コンデンサの端効果は無視できるものとする。

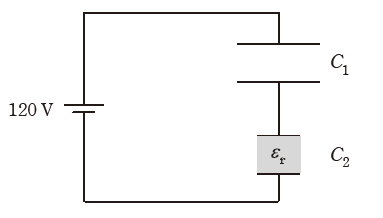
(a)　コンデンサC₂の誘電体の比誘電率ε_rの値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 1
2. 2
3. 3
4. 4
5. 5

(b)　C₁の静電容量が30μFのとき、C₁とC₂の合成容量の値[μF]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 10
2. 20
3. 30
4. 40
5. 50

 

 

 

 

 

　解 説　　　　

(a)

問題文で与えられた情報を問題の図に書き込むと、下図のようになります。なお、直列に並んだコンデンサに蓄えられる電荷Q[C]は等しくなります。また、ここではC₂の金属板の面積をS[m²]としています。

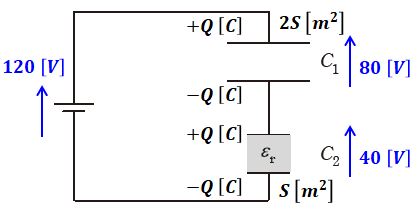
ここで、問われているのは比誘電率ε_rの値なので、(1)式に示す公式を使う必要があります。

• C：静電容量 [F]
• ε_r：比誘電率
• ε₀：真空の誘電率 [F/m]
• S：板の面積 [m²]
• d：板間距離 [m]

上式において、コンデンサC₁とC₂で与えられた情報を代入すると、次のようになります。なお、誘電体が挿入されていないコンデンサC₁ではε_rは無視できます(ε_r＝1)。

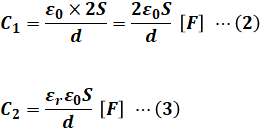
(2)式と(3)式を比べるとわかるように、静電容量C₁とC₂の比がわかれば、コンデンサC₂のε_rを求めることができそうです。

ここで、先に解説した通り、直列に並んだコンデンサに蓄えられる電荷Q[C]は等しくなるので、Q＝CV[C]の公式を使うと、次に示すように静電容量C₁、C₂の比からε_rを算出することができます。

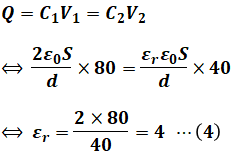
よって、正解は(4)となります。

(b)

問われているのはC₁とC₂の合成容量の値です。複数のコンデンサが直列に並んでいるとき、合成静電容量の逆数は、各々の静電容量の逆数の和と一致します。よって、合成静電容量Cは次のように表されます。

C₁の値はすでに30[μF]を与えられているので、C₂の値を求めて(5)式に代入すれば答えとなるCの値が得られます。

ここで、(4)式の最初の行で示した通り、Q＝C₁V₁＝C₂V₂が成り立つので、そこから次のようにしてC₂を求めることができます。

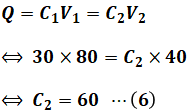
よって、(6)式を(5)式に代入すれば、合成容量Cを算出できます。

以上から、正解は(2)です。