電験三種 R4年度上期 理論 問16 問題と解説

　問 題　　　　　

図は、抵抗R_ab[kΩ]のすべり抵抗器、抵抗R_d[kΩ]、抵抗R_e[kΩ]と直流電圧E_s＝12Vの電源を用いて、端子H、G間に接続した未知の直流電圧[V]を測るための回路である。次の(a)及び(b)の問に答えよ。

ただし、端子Gを電位の基準(0V)とする。

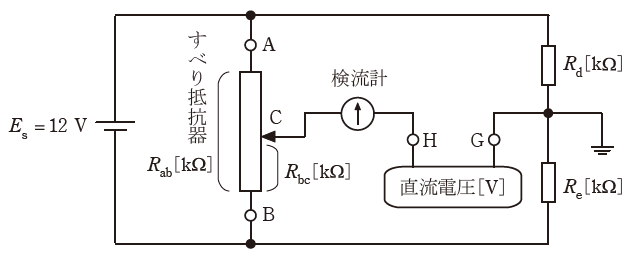
(a)　抵抗R_d＝5kΩ、抵抗R_e＝5kΩとして、直流電圧3Vの電源の正極を端子Hに、負極を端子Gに接続した。すべり抵抗器の接触子Cの位置を調整して検流計の電流を零にしたところ、すべり抵抗器の端子Bと接触子C間の抵抗R_bc＝18kΩとなった。

すべり抵抗器の抵抗R_ab[kΩ]の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 18
2. 24
3. 36
4. 42
5. 50

(b)　次に、直流電圧3Vの電源を取り外し、未知の直流電圧E_x[V]の電源を端子H、G間に接続した。ただし、端子Gから見た端子Hの電圧をE_x[V]とする。

抵抗R_d＝2kΩ、抵抗R_e＝22kΩとしてすべり抵抗器の接触子Cの位置を調整し、すべり抵抗器の端子Bと接触子C間の抵抗R_bc＝12kΩとしたときに、検流計の電流が零となった。

このときのE_x[V]の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. －5
2. －3
3. 0
4. 3
5. 5

 

 

 

 

 

　解 説　　　　

(a)

まず、設問(a)で与えられている情報をまとめると、問題の図は下図のような等価回路に描き換えることができます。

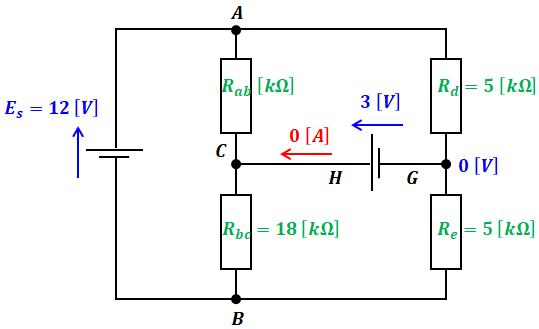
上図より、E_s＝12[V]とR_d＝R_e＝5[kΩ]から、R_dとR_eの端子電圧は6[V]ずつであることがわかります。また、両抵抗の間が接地点(＝0[V])なので、上図の各点における電圧を書き込むと、以下のようになります。

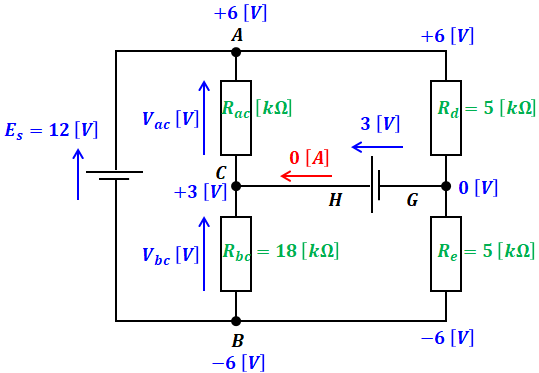
よって、R_abとR_bcのそれぞれの端子電圧V_ac、V_bcは次のように計算できます。

ここで、検流計の電流は0[A]なので抵抗R_acと抵抗R_bcには同じ電流Iが流れるため、これらの端子電圧の比がそのまま抵抗値の比となります。このことから、R_acの値を計算することができます。

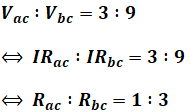
以上から、すべり抵抗器の抵抗R_ab[kΩ]の値は次のようになります。

よって、正解は(2)です。

(b)

設問(a)のときと同様、まずは設問(b)で与えられている情報を等価回路にまとめます。すると、下図のような等価回路で表すことができます。

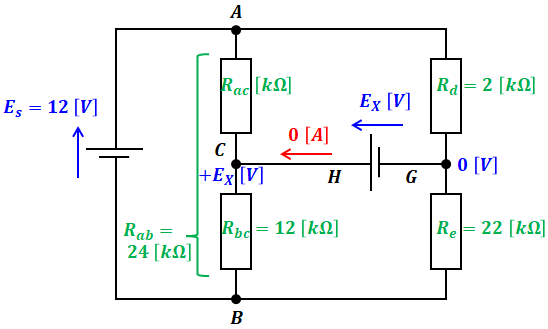
上図において、すべり抵抗器そのものは設問(a)でも設問(b)でも同じものを使っているので、この抵抗器全体の抵抗抵抗R_abは24[kΩ]です。よって、R_acは引き算ですぐに求めることができます(R_ac＝24－12＝12)。

すると、R_ac＝R_bc＝12[kΩ]となります。E_s＝12[V]なので、R_acとR_bcのそれぞれの端子電圧V_ac、V_bcはV_ac＝V_bc＝6[V]だとわかります。

また、R_dとR_eの抵抗値の比が2：22＝1：11なので、E_s＝12[V]より、R_dの端子電圧が1[V]、R_eの端子電圧が11[V]であることもわかります。ここで、両抵抗の間が接地点(＝0[V])なので、R_dの上側の電圧が＋1[V]、R_eの下側の電圧が－11[V]です。

以上をまとめると、先に示した回路図は以下のようになります。

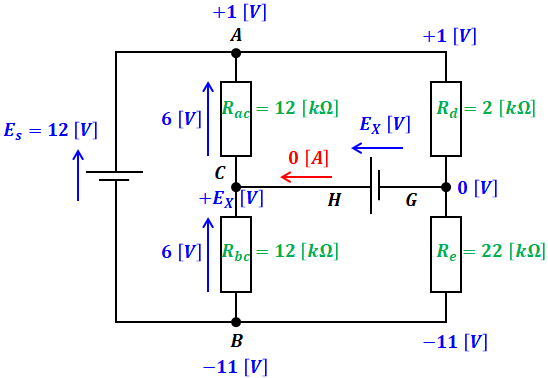
上図から、E_x[V]は、点Aの＋1[V]よりも6[V]低いところなので、次のように求めることができます。もちろん、点Bの－11[V]よりも6[V]高いところと考えても同じ答えが得られます。

よって、正解は(1)です。