問 題
図のように、線間電圧200Vの対称三相交流電源に、三相負荷として誘導性リアクタンスX=9Ωの3個のコイルとR[Ω]、20Ω、20Ω、60Ωの4個の抵抗を接続した回路がある。端子a、b、cから流入する線電流の大きさは等しいものとする。
この回路について、次の(a)及び(b)の問に答えよ。
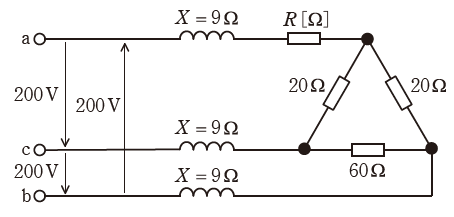
(a) 線電流の大きさが7.7A、三相負荷の無効電力が1.6kvarであるとき、三相負荷の力率の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.5
- 0.6
- 0.7
- 0.8
- 1.0
(b) a相に接続されたRの値[Ω]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 4
- 8
- 12
- 40
- 80
解 説
(a)
問われているのが力率cosθの値で、無効電力Q[kvar]の値が与えられているため、皮相電力S[kV・A]や有効電力P[kV]の値がわかれば、cosθの値を計算することができます。
ここで、すでに線間電圧や線電流の値がわかっているので、下式のように計算して三相交流回路の皮相電力Sを求めます。

よって、下図のような直角三角形から、有効電力Pと力率cosθを求めていきます。
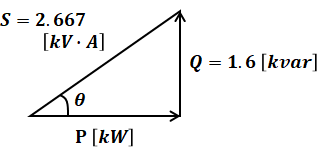

以上から、正解は(4)となります。
(b)
本問の三相交流回路は、Δ結線上の3つの抵抗のほかにa線上にも抵抗があって、一見すると見慣れない形となっています。しかし、電源が対称三相交流電源で、端子a、b、cから流入する線電流の大きさも等しいので、全体で見ると一般的な対称三相交流回路であるといえます。
ここで、a線上の抵抗とΔ結線上の3つの抵抗を並べて計算しやすくするため、まずはΔ-Y変換によってΔ結線をY結線に描き換えます。計算問題の場合には、大抵はY結線にしておいたほうが計算しやすいことが多いです。
Δ-Y変換は次に示すような計算によって行うことができます。なお、リアクタンスXについては三相ともすでに9[Ω]でバランスが取れているので、ここでは省略しています。
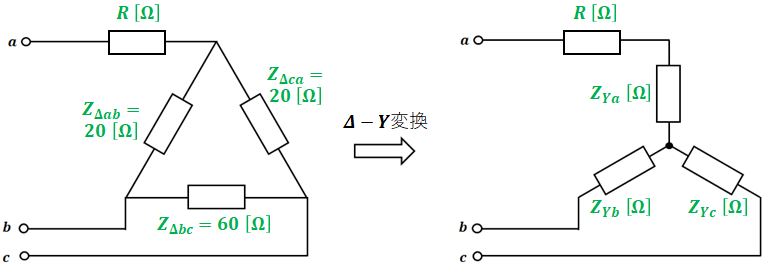
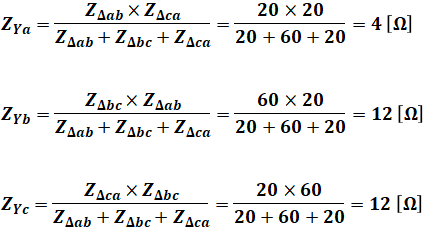
以上より、問題の図の右半分と以下の回路図は等価となります。
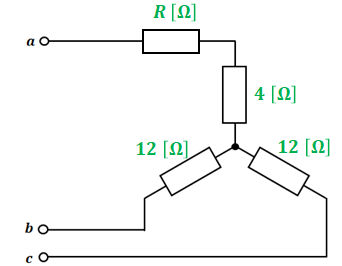
すでに解説した通り、これは対称三相交流回路なので、a,b,c相はいずれも等価です。よって、b相とc相にある抵抗の値が12[Ω]であるなら、a相で直列に並んでいる2つの抵抗の和も12[Ω]でなくてはなりません。
![]()
以上から、正解は(2)となります。

コメント