問 題
次の文章は、図1の回路の動作について述べたものである。
図1は、演算増幅器(オペアンプ)を用いたシュミットトリガ回路である。この演算増幅器には+5Vの単電源が供給されており、0Vから5Vまでの範囲の電圧を出力できるものとする。
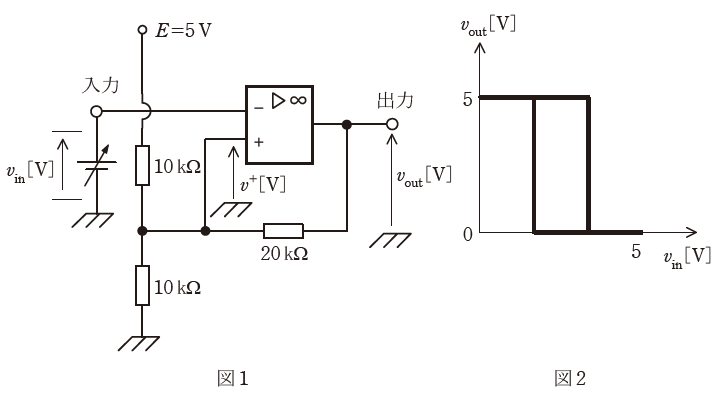
- 出力電圧voutは0~5Vの間にあるため、演算増幅器の非反転入力の電圧v+[V]は( ア )の間にある。
- 入力電圧vinを0Vから徐々に増加させると、vinが( イ )Vを上回った瞬間、voutは5Vから0Vに変化する。
- 入力電圧vinを5Vから徐々に減少させると、vinが( ウ )Vを下回った瞬間、voutは0Vから5Vに変化する。
- 入力vinに対する出力voutの変化を描くと、図2のような( エ )を示す特性となる。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
- ア イ ウ エ
- 1.25~3.75 3.75 1.25 位相遅れ
- 1.25~3.75 1.25 3.75 ヒステリシス
- 2~3 2 3 ヒステリシス
- 2~3 2.75 2.25 位相遅れ
- 2~3 3 2 ヒステリシス
解 説
( ア )に関して、まず演算増幅器の問題で重要なことは、理想的な演算増幅器は入力インピーダンスが無限大、増幅度も無限大、出力インピーダンスは零であることです。
そのため、計算上は演算増幅器に電流が流れないので、ここを無視して問題の図を下図のように描き換えて考えることができます。また、説明の都合上、下図の各点にA~D、各抵抗にR1~R3の記号を付けます。
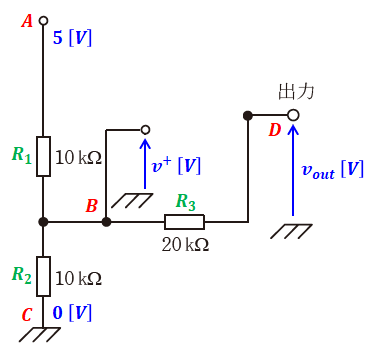
ここで問題文を読むと、voutは0[V]から5[V]までの範囲を変化することがわかります。
そこで、まずはvout=0[V]のときについて考えます。このとき、点Cと点Dがともに0[V]で、点Aが5[V]です。また、点Bを中心に5[V]側にR1があり、0[V]側にR2とR3が並列に並んでいるため、上図は下図のような等価回路に描き換えることができます。

( ア )にはv+[V]の範囲が入るので、求めたいのは上図におけるのv+値です。よって、まずは回路全体の合成抵抗Rを計算し、そこから電源や抵抗R1を流れる電流Iを求めます。そうするとR1の端子電圧V1がわかるので、電源電圧5[V]からそれを引けば、v+[V]を計算することができます。
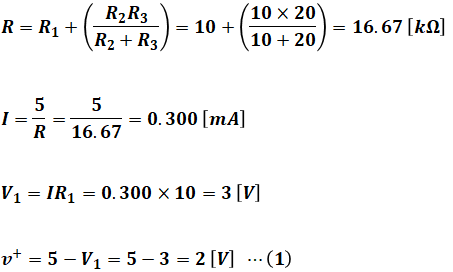
以上から、vout=0[V]のとき、v+=2[V]となります。
今度はvout=5[V]のときについて考えます。考え方や計算の仕方は先ほどと同様です。まずは等価回路を描いて、その後、次に示すような計算によってv+の値を算出します。
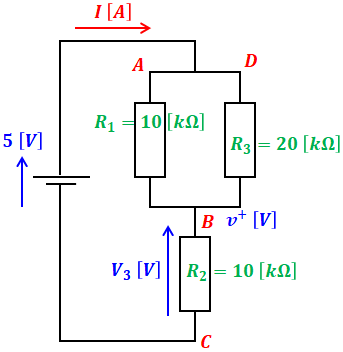
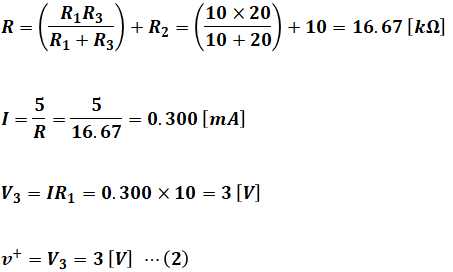
以上から、vout=5[V]のとき、v+=3[V]となります。
(1)、(2)式より、v+の値は2[V]~3[V]の間を動くので、( ア )には「2~3」が入ります。
( イ )に関して、問題の図2より、vinが0[V]から増加させると、しばらくはvout=5[V]であることが読み取れます。ここで、( ア )のところで計算した結果を踏まえると、このしばらくの間はv+=3[V]を保っていることがわかります。
よって、vinが0[V]から3[V]までの間はvout=5[V]が保たれ、vinが3[V]を超えた瞬間にvoutは反転して0[V]になります。つまり、( イ )には「3」が入ります。
( ウ )も同様に考えればよく、問題の図2より、vinが5[V]から減少させると、しばらくはvout=0[V]であることが読み取れます。( ア )の計算過程から、この間はv+=2[V]を保っていることがわかります。
よって、vinが5[V]から2[V]まで下がっている間はvout=0[V]が保たれ、vinが2[V]を下回った瞬間にvoutは反転して5[V]になります。つまり、( ウ )には「2」が入ります。
( エ )に関して、( イ )と( ウ )からわかるように、今回の場合、出力の結果が入力の値のみで決まるわけではなく、入力がどのような経過をたどったかが影響します。このような特性をヒステリシスというので、( エ )には「ヒステリシス」が入ります。
以上から、( ア )は「2~3」、( イ )は「3」、( ウ )は「2」、( エ )は「ヒステリシス」となるので、正解は(5)です。

コメント