電験三種 R4年度上期 理論 問10 問題と解説

　問 題　　　　　

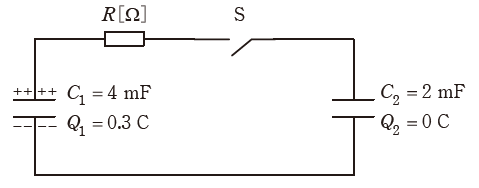
図の回路において、スイッチSが開いているとき、静電容量C₁＝4mFのコンデンサには電荷Q₁＝0.3Cが蓄積されており、静電容量C₂＝2mFのコンデンサの電荷はQ₂＝0Cである。この状態でスイッチSを閉じて、それから時間が十分に経過して過渡現象が終了した。

この間に抵抗R[Ω]で消費された電気エネルギー[J]の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 1.25
2. 2.50
3. 3.75
4. 5.63
5. 7.50

 

 

 

 

 

　解 説　　　　

スイッチSが開いているとき、2つのコンデンサの静電エネルギーの合計W_before[J]は次のように表すことができます。

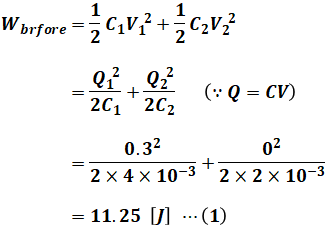
次に、スイッチSを閉じると回路に電流が流れます。そして抵抗Rでいくらかの電気エネルギーが消費されたのち、時間が十分に経過すると回路に電流は流れなくなります。

過渡現象が終了した状態では電流が流れていないので、抵抗Rの両端の電圧は0[V]であり、抵抗Rはただの導体と見なすことができます。よって、閉回路にある2つのコンデンサの端子電圧V’₁、V’₂の値は等しくなります。

静電容量Cの値は定数のためスイッチ操作の前後において不変であるので、コンデンサQ＝CVの公式を用いると、(2)式は次に示す(3)式に変形できます。

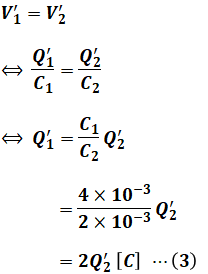
ここで、スイッチの開閉前後で電荷が移動することはあっても、回路全体で見れば、その総量は変わりません。つまり、スイッチ操作前の電荷の総量と、スイッチ操作後の電荷の総量は等しくなります。

よって、(3)式の結果を(4)式に代入すると、電荷Q’₁、Q’₂の具体的な値を求めることができます。

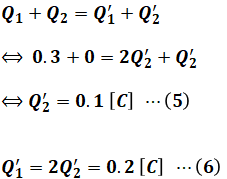
(5)式と(6)式から、過渡現象が終了した状態の2つのコンデンサの静電エネルギーの合計W_after[J]は次のように計算できます。

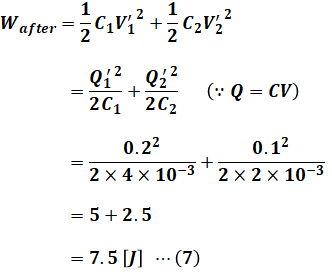
以上より、(1)式で求めたW_before[J]と(7)式で求めたW_after[J]の差が抵抗R[Ω]で消費された電気エネルギーW_R[J]の値となるので、次のように計算することで答えが出ます。

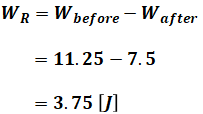
よって、正解は(3)です。