電験三種 R4年度上期 理論 問9 問題と解説

　問 題　　　　　

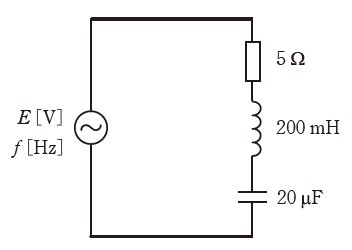
図のように、5Ωの抵抗、200mHのインダクタンスをもつコイル、20μFの静電容量をもつコンデンサを直列に接続した回路に周波数f[Hz]の正弦波交流電圧E[V]を加えた。

周波数fを回路に流れる電流が最大となるように変化させたとき、コイルの両端の電圧の大きさは抵抗の両端の電圧の大きさの何倍か。最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 5
2. 10
3. 15
4. 20
5. 25

 

 

 

 

 

　解 説　　　　

RLC直列回路において電流が最大となるのは、誘導性リアクタンスX_Lと容量性リアクタンスX_Cの大きさが等しくなり(X_L＝X_C)、その作用が互いに打ち消し合って回路のインピーダンスZが最小(Z＝R)になるときです。

このように、X_L＝X_Cによって回路のインピーダンスZが小さくなり、大きな電流が流れるようになる現象を直列共振といいます。そして、直列共振の条件式は以下のように表されます。

上式は公式として覚えておくと便利ですが、もし導出を含めて理解しておきたい場合には、RLC直列共振回路のページを参照してください。

(1)式において、問題文で与えられているL＝200[mH]、C＝20[μF]を使えば、次に示す通り周波数f[Hz]を求めることができます。

ここで、問われているのは直列共振のときのコイルの両端の電圧V_L[V]と抵抗の両端の電圧V_R[V]の大きさの比です。回路に流れる電流をI[A]とすると、その比は(2)式を使って以下のように算出することができます。なお、抵抗Rは問題文より5[Ω]です。

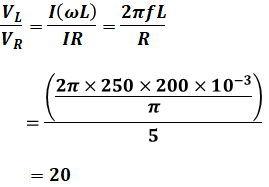
よって、正解は(4)となります。