電験三種 R4年度上期 理論 問3 問題と解説

　問 題　　　　　

図のような環状鉄心に巻かれたコイルがある。

図の環状コイルについて、

• 端子1－2間の自己インダクタンスを測定したところ、40mHであった。
• 端子3－4間の自己インダクタンスを測定したところ、10mHであった。
• 端子2と3を接続した状態で端子1－4間のインダクタンスを測定したところ、86mHであった。

このとき、端子1－2間のコイルと端子3－4間のコイルとの間の結合係数kの値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 0.81
2. 0.90
3. 0.95
4. 0.98
5. 1.8

 

 

 

 

 

　解 説　　　　

本問のように環状鉄心に2つのコイルが巻かれている場合、それぞれのコイルに自己インダクタンスL[H]が生じるほか、相互誘導起電力によって相互インダクタンスM[H]が生じます。

本問で問われているのは結合係数kの値ですが、これは相互インダクタンスMと自己インダクタンスLをつなぐ下式に登場するパラメータです。これは公式として押さえておきたい重要事項です。

• M：相互インダクタンス [H]
• k：結合係数(0～1)
• L₁、L₂：左右それぞれの自己インダクタンス [H]

上式に関して、問題文で与えられているのは、端子1－2間の自己インダクタンスL₁＝40[mH]と、端子3－4間の自己インダクタンスL₂＝10[mH]です。よって、あとは相互インダクタンスMを求めれば結合定数kが計算できます。

問題文には3つ目の条件として「端子2と3を接続した状態で端子1－4間のインダクタンスを測定したところ、86mHであった。」と書かれています。つまり、端子1→2→3→4とつないだときの合成インダクタンスが86[mH]ということです。

この合成インダクタンスとは、自己インダクタンスと相互インダクタンスを合わせたものです。ただし、2つのコイルの接続の仕方によってこの値が変わってきます。

2つのコイルで発生する磁束の向きが同じ方向(強め合う方向)となるような接続の仕方を、和動接続といいます。反対に、2つのコイルでの磁束が打ち消し合って弱め合うような接続の仕方を、差動接続といいます。

和動接続と差動接続のそれぞれについて、合成インダクタンス(L_wa、L_sa)は次の式で表すことができます。

• L_wa：和動接続での合成インダクタンス [H]
• L_sa：差動接続での合成インダクタンス [H]
• L₁、L₂：左右それぞれの自己インダクタンス [H]
• M：相互インダクタンス [H]

今回の場合は下図のように接続するので、右ねじの法則を使うと、それぞれのコイルで発生する磁束φは同じ方向を向いていることがわかります。

よって、問題文で与えられた各数値を、和動接続の(2)式に代入します。

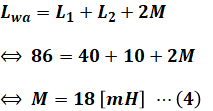
そして(4)式を(1)式に代入することで、求めたいkを算出することができます。

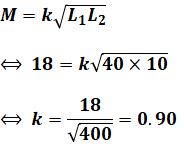
以上から、正解は(2)となります。