電験三種 R4年度上期 理論 問2 問題と解説

　問 題　　　　　

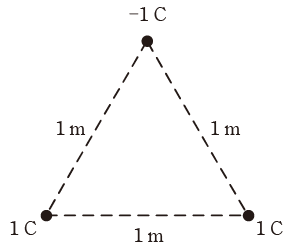
真空中において、図に示すように一辺の長さが1mの正三角形の各頂点に1C又は－1Cの点電荷がある。

この場合、正の点電荷に働く力の大きさF₁[N]と、負の点電荷に働く力の大きさF₂[N]の比F₂/F₁の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. √2
2. 1.5
3. √3
4. 2
5. √5

 

 

 

 

 

　解 説　　　　

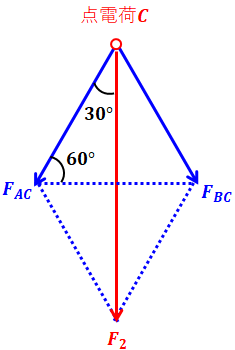
2つの点電荷の間には静電気力が発生しますが、正電荷と正電荷の間には斥力(反発し合う力)が働き、正電荷と負電荷の間には引力が働きます。よって、3つの点電荷をA,B,Cとすると、静電気力の向きは下図のように表すことができます。

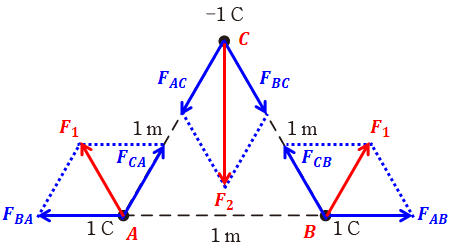
上図において、F_BAは点電荷Bから点電荷Aが受ける静電気力を表していると思ってください。F_ACなども同様です。また、問題文で指定されているF₁、F₂は上図の赤矢印で表しています。

ここで、2つの点電荷の間に働く静電気力は以下の式で示されます。

• F：静電気力 [N]
• ε₀：真空の誘電率　8.854×10^-12[F/m]
• Q：電荷 [C]
• r：電荷間の距離 [m]

今回の場合は点電荷A,B,Cともに電荷の大きさと互いの距離がそれぞれ等しいため、2つの点電荷の間に働く静電気力の大きさは次のように共通の値となります(向きは異なります)。

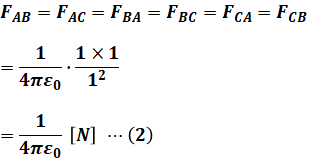
上図と(1)式から、F₁、F₂はそれぞれ次のように計算することができます。

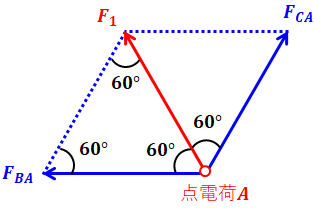
問われているのは比F₂/F₁の値なので、(3)式、(4)式より、比F₂/F₁は次のようになります。

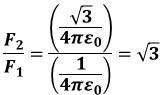
よって、正解は(3)です。