問 題
面積がともにS[m2]で円形の二枚の電極板(導体平板)を、互いの中心が一致するように間隔d[m]で平行に向かい合わせて置いた平行板コンデンサがある。電極板間は誘電率ε[F/m]の誘電体で一様に満たされ、電極板間の電位差は電圧V[V]の直流電源によって一定に保たれている。
この平行板コンデンサに関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし、コンデンサの端効果は無視できるものとする。
- 誘電体内の等電位面は、電極板と誘電体の境界面に対して平行である。
- コンデンサに蓄えられる電荷量は、誘電率が大きいほど大きくなる。
- 誘電体内の電界の大きさは、誘電率が大きいほど小さくなる。
- 誘電体内の電束密度の大きさは、電極板の単位面積当たりの電荷量の大きさに等しい。
- 静電エネルギーは誘電体内に蓄えられ、電極板の面積を大きくすると静電エネルギーは増大する。
解 説
問題文の条件を回路図で表すと、下図のように描くことができます。
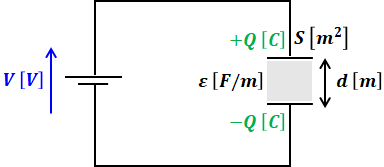
上図を見ながら、各選択肢の正誤を考えていきます。
選択肢(1)で、上図の通り電極板(下)の電圧は0[V]、電極板(上)の電圧はV[V]です。電極板間の誘電率εは一定なので、電極板間の電位は電極板(下)から電極板(上)に向かって、距離に対して比例の関係で上がっていきます。
そのため、電極板から等しい距離にある点の集合体が等電位面となるので、等電位面は電極板と誘電体の境界面に対して平行となります。よって、選択肢(1)は正しいです。
選択肢(2)で、電荷Q[C]は静電容量C[F]と電圧V[V]を使って以下の(1)式で表されます。
![]()
- Q:電荷 [C]
- C:静電容量 [F]
また、静電容量C[F]は問題文で与えられている各パラメータを使って(2)式の通り表すことができます。
![]()
- ε:誘電率 [F/m]
- S:板の面積 [m2]
- d:板間距離 [m]
(2)式を(1)式に代入すると、次の(3)式のようになります。
![]()
(3)式より、電荷Qは誘電率εに比例することがわかるので、選択肢(2)は正しいといえます。
選択肢(3)で、電界E[V/m]は次の(4)式で求めることができます。
![]()
- E:電界の強さ [V/m]
- V:電圧 [V]
- d:板間距離 [m]
ここで、電圧Vと板間距離dはいずれも問題文から一定の値であることがわかります。右辺にあるこれらの数値は誘電率εの値が変わったとしても不変なので、左辺の電界Eも誘電率εに影響しません。
よって、選択肢(3)の記述が誤りなので、これが正解となります。
選択肢(4)で、電束密度というのは1[m2]あたりの電束の数です。誘電体内の電束密度の大きさは、電極板の単位面積当たりの電荷量の大きさに等しいので、選択肢(4)は正しい記述です。
選択肢(5)で、コンデンサに蓄えられる静電エネルギーWは以下の(5)式で表されます。
![]()
ここでは静電エネルギーWと電極板の面積Sとの関係が問われているので、(2)式を(5)式に代入します。
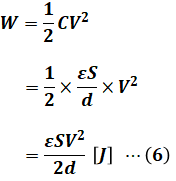
(6)式より、WとSは比例の関係にあるため、選択肢(5)は正しい記述です。
以上から、正解は(3)となります。

コメント