電験三種 R4年度上期 機械 問17 問題と解説

　問 題　　　　　

消費電力1.00kWのヒートポンプ式電気給湯器を6時間運転して、温度20.0℃、体積0.370m³の水を加熱した。ここで用いられているヒートポンプユニットの成績係数(COP)は4.5である。次の(a)及び(b)の問に答えよ。

ただし、水の比熱容量と密度は、それぞれ、4.18×10³J/(kg･K)と1.00×10³kg/m³とし、水の温度に関係なく一定とする。

ヒートポンプ式電気給湯器の貯湯タンク、ヒートポンプユニット、配管などの加熱に必要な熱エネルギーは無視し、それらからの熱損失もないものとする。

また、ヒートポンプユニットの消費電力及びCOPは、いずれも加熱の開始から終了まで一定とする。

(a)　このときの水の加熱に用いた熱エネルギーの値[MJ]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 21.6
2. 48.6
3. 72.9
4. 81.0
5. 97.2

(b)　加熱後の水の温度[℃]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 34.0
2. 51.4
3. 67.1
4. 72.4
5. 82.8

 

 

 

 

 

　解 説　　　　

(a)

まず、問題文よりヒートポンプユニットのCOP(成績係数)は4.5です。成績係数(COP)とは、ヒートポンプの効率を示す指標で、消費電力量Wに対する得られた熱エネルギーQで表されます。

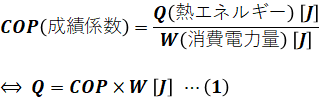
今回問われているのは熱エネルギーQなので、上式より、消費電力量Wを求めればQが計算できることがわかります。

ここで、消費電力量W[J]は、消費電力P＝1.00[kW]と加熱した時間t＝6[h]から、次のように計算できます。なお、以下の計算過程では電力の単位を[W]、時間の単位を[s]に直してから計算しています。

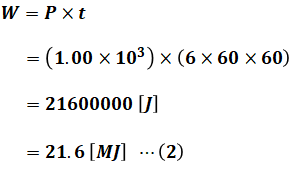
よって、(2)式の結果を(1)式に代入すると、求めたい熱エネルギーQを算出することができます。

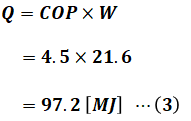
以上から、正解は(5)となります。

(b)

まず、水の密度が1.00×10³kg/m³なので、水0.370m³の質量は次のように計算できます。

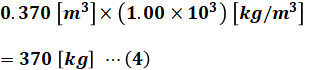
設問(a)で求めた(3)式の熱量を使うと、この370[kg]の水を何度まで加熱することができるか…というのが、設問(b)の趣旨です。これは、以下に示す等式を使って求めることができます。公式として覚えていなくても単位に注目すればわかりやすいと思います。

なお、比熱容量のところに出てくる[K](ケルビン)は[℃]に置き換えられる点がポイントです。Kは絶対温度、℃は摂氏として使われますが、「温度差」として用いる限りは両者を区別する必要はありません。

• Q：熱量 [J]
• c：比熱容量 [J/kg・℃]
• m：物質の重量 [kg]
• Δθ：上昇温度 [℃]

求めたい加熱後の水の温度をθ[℃]とすると、(5)式に(3)式や(4)式、問題文で与えられた数値を代入して計算すれば、θを次のように求めることができます。

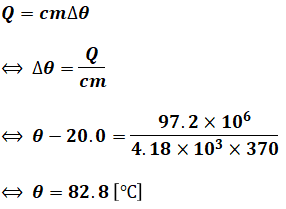
よって、正解は(5)となります。