電験三種 R4年度上期 法規 問13 問題と解説

　問 題　　　　　

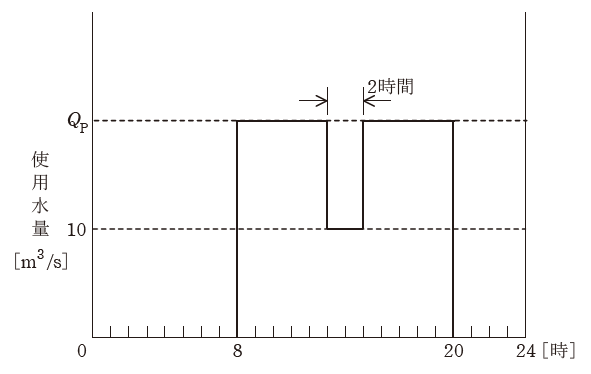
有効落差80mの調整池式水力発電所がある。調整池に取水する自然流量は10m³/s一定であるとし、図のように1日のうち12時間は発電せずに自然流量の全量を貯水する。

残り12時間のうち2時間は自然流量と同じ10m³/sの使用水量で発電を行い、他の10時間は自然流量より多いQ_p[m³/s]の使用水量で発電して貯水分全量を使い切るものとする。

このとき、次の(a)及び(b)の問に答えよ。

(a)　運用に最低限必要な有効貯水量の値[m³]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 220×10³
2. 240×10³
3. 432×10³
4. 792×10³
5. 864×10³

(b)　使用水量Q_p[m³/s]で運転しているときの発電機出力の値[kW]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、運転中の有効落差は変わらず、水車効率、発電機効率はそれぞれ90%、95%で一定とし、溢水(いっすい)はないものとする。

1. 12400
2. 14700
3. 16600
4. 18800
5. 20400

 

 

 

 

 

　解 説　　　　

(a)

問題文より、発電を終えた20時には貯水分全量を使い切って貯水量が0[m³]になり、20時から翌朝の8時までは自然流量10[m³/s]のペースで貯水していくことがわかります。そして8時から20時までは発電することでまた調整池が空になって24時間サイクルが1周します。

よって、最低限必要な貯水量V[m³]というのは、20時から翌朝の8時までの12時間(＝60×60×12[s])に調整池に溜まっていく水の量ということになります。自然流量は10[m³/s]なので、これは以下のように計算することができます。

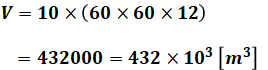
以上から、正解は(3)です。

(b)

水力発電において、使用水量Q[m³/s]で運転しているときの発電機出力P[kW]は、次の式で表すことができます。これは重要事項として押さえておくべき公式です。

• P：発電機出力 [kW]
• Q：流量 [m³/s]
• H：有効落差 [m]
• η_t：水車効率
• η_g：発電機効率

(1)式において、今回の場合はすでにH＝80、η_t＝0.90、η_g＝0.95とわかっているので、流量Q(本問の場合はQ_p)がいくつであるかを考えれば答えが出せます。

Q_pを求める方法はいくつかありますが、ここではそのうち一例を挙げて解説します。もし以下の解説と異なる計算をしていた場合でも、最終的なQ_pの値が合っていればしっかり理解できていると思うので、心配しなくて大丈夫です。

まず、調整池に水が溜まる分について考えると、自然流量は10[m³/s]なので、24時間の間に溜まる水量V_inは次のようになります。

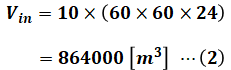
水力発電によって消費する水量も、24時間の間には(2)式と同様に864000[m³]となります。しかし、時間帯によって使われる量が異なるため、下図のように分けて考えていきます。

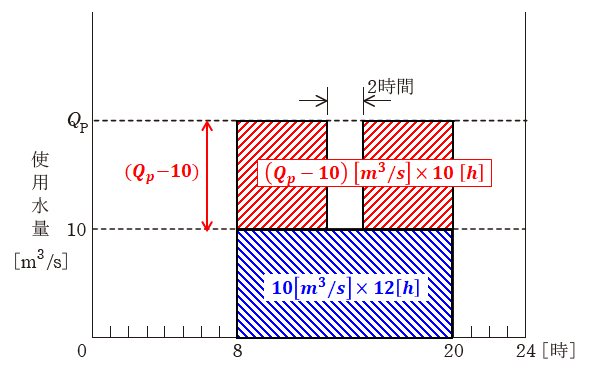
上図の青色部分について、時間あたりの使用水量は10[m³/s]、時間は8時から20時までの12時間なので、この範囲での総使用水量は次のようになります。

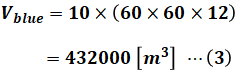
一方、赤色部分について、使用水量は(Q_p－10)[m³/s]、時間は8時から20時までのうち2時間を引いた10時間となります。そのため、この範囲での総使用水量は次のように表すことができます。

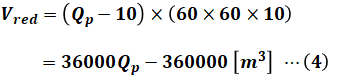
よって、溜まる水量である(2)式と、消費する水量である(3)式・(4)式の合計が一致するので、これらを等式で結んで計算すれば、Q_pを算出することができます。

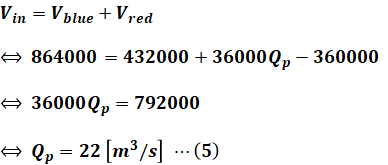
これでQ_pが求められたので、(5)式と設問で与えられた各数値を(1)に代入すれば、発電機出力P[kW]を計算することができます。

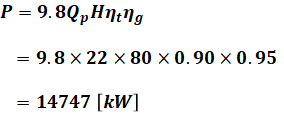
以上から、正解は(2)となります。