電験三種 R3年 理論 問15 問題と解説

　問 題　　　　　

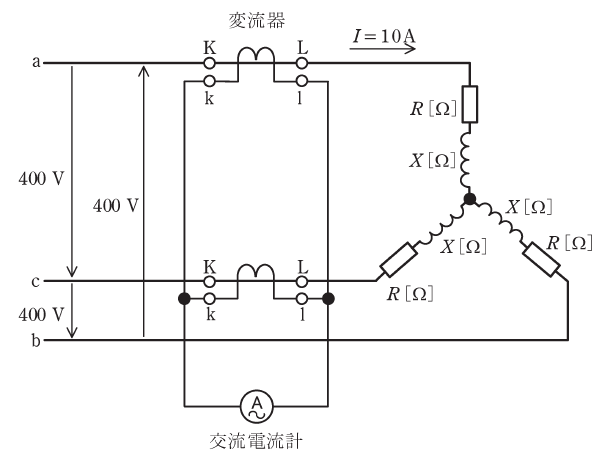
図のように、線間電圧400Vの対称三相交流電源に抵抗R[Ω]と誘導性リアクタンスX[Ω]からなる平衡三相負荷が接続されている。平衡三相負荷の全消費電力は6kWであり、これに線電流I＝10Aが流れている。

電源と負荷との間には、変流比20：5の変流器がa相及びc相に挿入され、これらの二次側が交流電流計を通して並列に接続されている。この回路について、次の(a)及び(b)の問に答えよ。

(a)　交流電流計の指示値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 0
2. 2.50
3. 4.33
4. 5.00
5. 40.0

(b)　誘導性リアクタンスXの値[Ω]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 11.5
2. 20.0
3. 23.1
4. 34.6
5. 60.0

 

 

 

 

 

　解 説　　　　

(a)

この回路は、対称三相交流電源に平衡三相負荷が接続されているため、a相、b相、c相を流れる電流は全て10[A]で、位相差がそれぞれ120°ずつずれています。

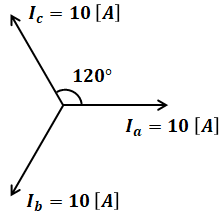
ここで、変流器はa相とc相に接続されているので、上図からI_aとI_cの合力I_acを考えます。

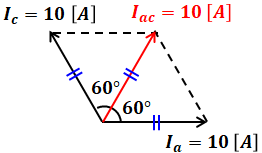
以上は三相回路での話(変流器の一次側)ですが、問われているのは交流電流計の指示値[A]であり、電流計は変流比20：5の変流器の二次側にあるため、指示値は次のようになります。

よって、正解は(2)です。

(b)

三相回路は1相分の等価回路を取り出して考えるとわかりやすいです。問題の図から、1相分の等価回路は以下のように描くことができます。

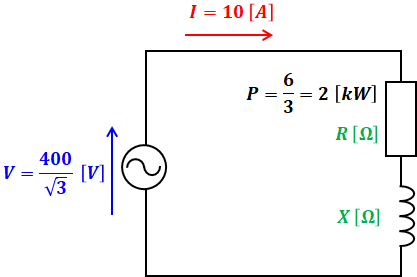
上記において、相電圧は線間電圧の1/√3で、消費電力(抵抗での有効電力)は3相分の1/3です。

電流Iと消費電力Pがわかっているので、抵抗Rは次のように計算できます。

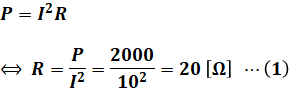
また、RとXを合わせた負荷全体の力率をcosθとすると、消費電力Pは次のようにも表せるので、これをcosθについて解けば力率がわかります。

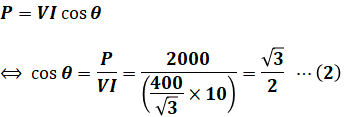
(1)式から抵抗R＝20[Ω]であり、(2)式から抵抗R、誘導性リアクタンスX、その合力(インピーダンス)Zの比は下図のようになるので、以下の計算によってXの値[Ω]を求めることができます。

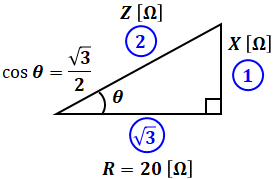
以上から、正解は(1)です。