問 題
開放電圧がV[V]で出力抵抗が十分に低い直流電圧源と、インダクタンスがL[H]のコイルが与えられ、抵抗R[Ω]が図1のようにスイッチSを介して接続されている。
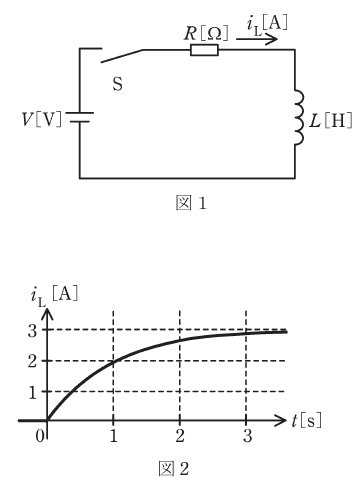
時刻t=0でスイッチSを閉じ、コイルの電流iL[A]の時間に対する変化を計測して、波形として表す。R=1Ωとしたところ、波形が図2であったとする。
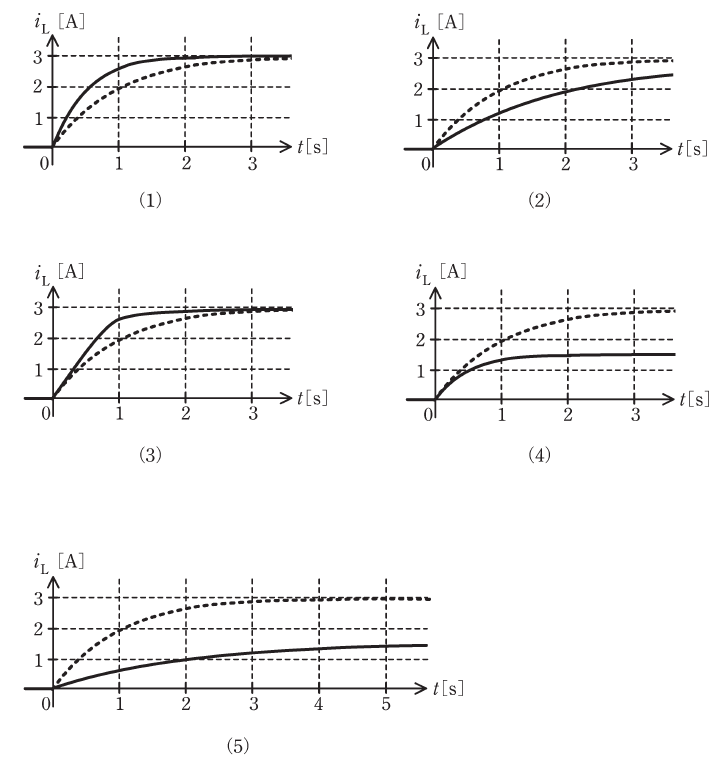
R=2Ωであればどのような波形となるか、波形の変化を最も適切に表すものを次の(1)~(5)のうちから一つ選べ。
ただし、選択肢の図中の点線は図2と同じ波形を表し、実線はR=2Ωのときの波形を表している。
解 説
各選択肢の違いは、次の2点です。
- 最終的な電流iLの値
- 上記1.に至るまでの時間
まずは上記1.について考えます。
図2より、R=1[Ω]のときには、最終的に電流iLは3[A]となります。十分に時間が経ったこの段階ではコイルはただの導線と見なせるので、オームの法則より、電源電圧は3[V]だとわかります。
一方、問われているのはR=2[Ω]のときですが、電源電圧は変わらないので3[V]です。よって、十分に時間が経ったときには、電流iLは1.5[A]となります。
以上から、この時点で選択肢は(4)と(5)の2つに絞られます。
続いて、上記2.について考えます。
電流や電圧(今回は電流)が立ち上がってから最大値(定常状態)の約63.2%になるまでに掛かった時間を、「時定数τ」といいます。
RL直列回路における時定数τの式は、以下のように表すことができます。
![]()
ちなみに、本問とは関係ありませんが、RC直列回路における時定数τの式は、以下のように表すことができます。
![]()
(1)式より、Rが1[Ω]から2[Ω]になった場合、時定数τは半分(1/2)になることがわかります。今回の場合、図2よりR=1[Ω]のときにはτ≒1[s]と読み取れるので、R=2[Ω]のときにはτ≒0.5[s]となります。
ここで、時定数τのときの電流値は、最大値の約63.2%です(これは条件に寄らない決まりごとです)。R=2[Ω]の場合の電流iLの最大値は1.5[A]なので、時定数τ≒0.5[s]のときの電流値iLτは次のようになります。
![]()
よって、選択肢(4)と(5)のうち、時定数τ≒0.5[s]のときの電流値iLτが0.948(≒1)[A]であるほうが適切なので、正解は(4)だと判断できます。

コメント