電験三種 R3年 理論 問4 問題と解説

　問 題　　　　　

次の文章は、電磁誘導に関する記述である。

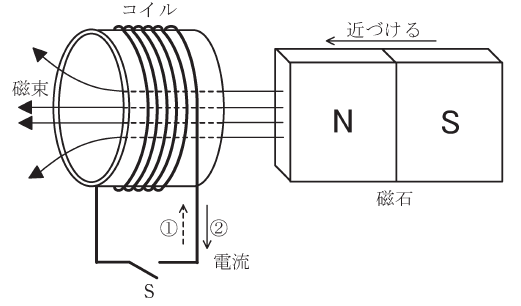
図のように、コイルと磁石を配置し、磁石の磁束がコイルを貫いている。

1．スイッチSを閉じた状態で磁石をコイルに近づけると、コイルには(　ア　)の向きに電流が流れる。

2．コイルの巻数が200であるとする。スイッチSを開いた状態でコイルの断面を貫く磁束を0.5sの間に10mWbだけ直線的に増加させると、磁束鎖交数は(　イ　)Wbだけ変化する。また、この0.5sの間にコイルに発生する誘導起電力の大きさは(　ウ　)Vとなる。ただし、コイル断面の位置によらずコイルの磁束は一定とする。

上記の記述中の空白箇所(ア)～(ウ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

　　　　ア　　イ　　 ウ

1. 　①　　2　　　 2
2. 　①　　2　　　 4
3. 　①　　0.01　　2
4. 　②　　2　　　 4
5. 　②　　0.01　　2

 

 

 

 

 

　解 説　　　　

(　ア　)に関して、電磁誘導では、磁束の変化を妨げるような方向に電流が流れます。つまり、問題の図のように外的要因(磁石)によって左向きの磁束が増えたのであれば、電磁誘導では逆に右向きの磁束を増やすように電流が流れます。

また、コイルを流れる電流の向きと磁束の向きは右ねじの法則に従います。親指(磁束)を右に向けたとき、残り4本の指(電流)を丸めると奥から手前にくるため、電流は奥から手前、つまり②の方向に流れることがわかります。よって、(　ア　)は「②」です。

(　イ　)を含む文章を読むと、コイルの巻数Nが200であること、磁束の増加分ΔΦは10[mWb]であることがわかります。よって、200個の円形コイルがそれぞれ10[mWb]ずつ増加すると考えることができるため、磁束鎖交数の変化は次のように計算できます。

よって、(　イ　)には「2」が入ります。

(　ウ　)について、電磁誘導によって発生する電圧のことを誘導起電力といい、その大きさは以下の式で表されます。

• E：誘導起電力 [V]
• N：巻数
• ΔΦ：磁束の増加分 [Wb]
• Δt：時間 [s]

上式に各数値を代入して計算すると、

となるので、誘導起電力の大きさは4[V]です。よって、(　ウ　)には「4」が入ります。

以上から、(　ア　)は「②」、(　イ　)は「2」、(　ウ　)は「4」となるので、正解は(4)です。