問 題
次の文章は、単相半波ダイオード整流回路に関する記述である。
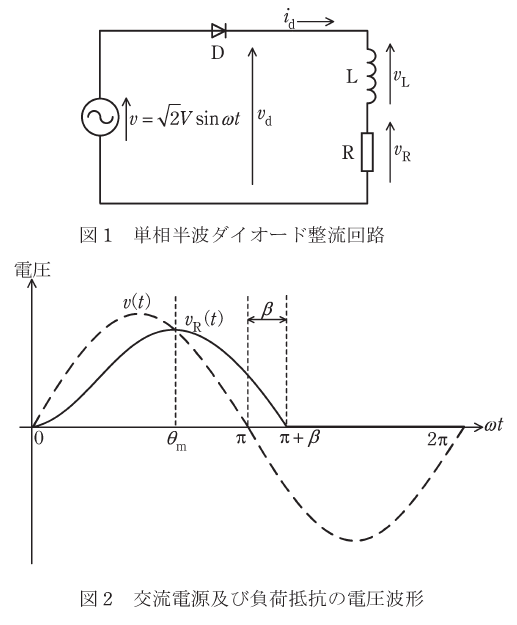
抵抗RとリアクトルLとを直列接続した負荷に電力を供給する単相半波ダイオード整流回路を図1に示す。また図1に示した回路の交流電源の電圧波形v(t)を破線で、抵抗Rの電圧波形vR(t)を実線で図2に示す。ただし、ダイオードDの電圧降下及びリアクトルLの抵抗は無視する。
次の(a)及び(b)の問に答えよ。
ただし、必要であれば次の計算結果を利用してよい。
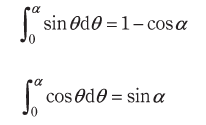
(a) 以下の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
図1の電源電圧v(t)>0の期間においてダイオードDは順方向バイアスとなり導通する。
v(t)とvR(t)が等しくなる電源電圧v(t)の位相をωt=θmとすると、出力電流id(t)が増加する電源電圧の位相ωtが0<ωt<θmの期間においては( ア )、ωt=θm以降については( イ )となる。
出力電流id(t)は電源電圧v(t)が負となってもv(t)=0の点よりもωt=βに相当する時間だけ長く流れ続ける。すなわち、Lの磁気エネルギーが( ウ )となるωt=π+βで出力電流id(t)が0となる。
出力電圧vd(t)の平均値Vdは電源電圧v(t)を0~( エ )の区間で積分して一周期である2πで除して計算でき、このときLの電圧vL(t)を同区間で積分すれば0となるので、Vdは抵抗Rの電圧vR(t)の平均値VRに等しくなる。
- ア イ ウ エ
- vL(t)>0 vL(t)<0 0 π+β
- vL(t)<0 vL(t)>0 0 π+β
- vL(t)>0 vL(t)<0 最大 π+β
- vL(t)<0 vL(t)>0 最大 β
- vL(t)>0 vL(t)<0 0 β
(b) 小問(a)において、電源電圧の実効値100V、β=π/6のときの出力電圧vd(t)の平均値Vd[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 3
- 20
- 42
- 45
- 90
解 説
(a)
( ア )と( イ )について、図1の回路図を見ると「v=vL+vR」が成り立つことがわかります。一方で図2を見ると、ωtが0<ωt<θmの期間では「v(t)>vR(t)」であり、ωt=θm以降では逆転して「v(t)≦vR(t)」となることがわかります。
よって、ωtが0<ωt<θmの期間ではvL(t)が正になり、ωt=θm以降ではvL(t)が負になると判断できるため、( ア )には「vL(t)>0」、( イ )には「vL(t)<0」を入れるのが適切です。
( ウ )に関して、この回路にはダイオードDがあるため、出力電流id(t)は時計回りにしか流れません。電源電圧v(t)が正の間はもちろんid(t)が流れますが、v(t)が負となってもリアクトルLにエネルギーが蓄えられている間はid(t)が流れ続けます。
さらに少し経ってLに蓄えられたエネルギーを使い切ったら、電源からもリアクトルからもエネルギーは供給されないため、id(t)が0となります。
よって、( ウ )には「0」が入ります。
( エ )について、( エ )を含む文章の最後にあるように、出力電圧vd(t)の平均値Vdは抵抗Rの電圧vR(t)の平均値VRと等しいです。よって、図2から平均値VRの平均値がどうなるかを考えるとわかりやすいと思います。
図2より、vR(t)の周期は2πで、0<ωt<π+βでvR(t)は正、π+β≦ωt≦2πでvR(t)は0となっています。よって、平均値VRは正の部分の積分値を2πで割ればよいので、( エ )には「π+β」が入ると判断できます。
以上から、( ア )には「vL(t)>0」が、( イ )には「vL(t)<0」、( ウ )には「0」が、( エ )には「π+β」が入るので、正解は(1)です。
(b)
問題文の( エ )を含む文章の前半部分と設問(a)の答えから、出力電圧vd(t)の平均値Vdは電源電圧v(t)を0~π+βの区間で積分して一周期である2πで除して計算できます。
また、電源は交流電源なので、サイン(sin)カーブを描きます。よって、平均値Vdは次の式で表すことができます。ここで、下式のVmaxは電源電圧v(t)の最大値であり、これは実効値の√2倍となります。
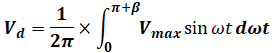
上式に設問(b)で与えられた数値を代入して、問題文で与えられたsinθの計算結果を使いつつ計算を進めていけば、求める答えを算出することができます。
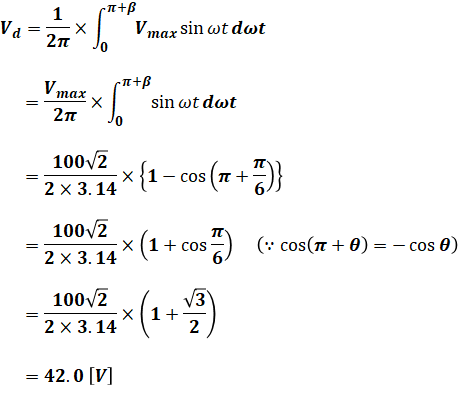
以上から、正解は(3)です。

コメント