問 題
需要家A~Cにのみ電力を供給している変電所がある。
各需要家の設備容量と、ある1日(0~24時)の需要率、負荷率及び需要家A~Cの不等率を表に示す値とする。表の記載に基づき、次の(a)及び(b)の問に答えよ。
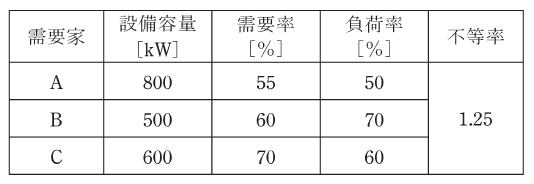
(a) 3需要家A~Cの1日の需要電力量を合計した総需要電力量の値[kW・h]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 10480
- 16370
- 20460
- 26650
- 27840
(b) 変電所から見た総合負荷率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、送電損失、需要家受電設備損失は無視するものとする。
- 42
- 59
- 62
- 73
- 80
解 説
設問の解説をする前に、まずは問題の表に出てくる需要率、負荷率、不等率について説明しておきます。
需要率は、「設備容量の合計値」に対する「最大需要電力」で表されます。

不等率は、「合成最大需要電力」に対する「各負荷の最大需要電力の合計値」で表されます。

負荷率は、「最大需要電力」に対する「平均需要電力」で表されます。

以上を押さえておけば計算問題には対応できると思いますが、より詳しく知りたい場合は需要率・不等率・負荷率のページを参照してください。
(a)
3需要家の総需要電力量を求める問題なので、各需要家の需要電力量[kW・h]をそれぞれ計算し、最後に合算します。
まず、問題の表を確認すると各需要家の設備容量[kW]がわかっています。解説の冒頭で示した通り、これに需要率(設備容量に対する最大需要電力)を掛けると、最大需要電力[kW]が算出されます。さらに負荷率(最大需要電力に対する平均需要電力)を掛けると、平均需要電力[kW]がわかります。
知りたいのは1日分の需要電力量[kW・h]ですが、これは平均需要電力[kW]に24[h]を掛けたものです。

よって、各需要家の需要電力量[kW・h]をそれぞれ次のようになります。
- A:
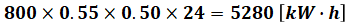
- B:

- C:
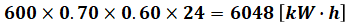
以上の和が、3需要家の総需要電力量となります。
![]()
よって、正解は(2)です。
(b)
総合負荷率が問われているため、解説の冒頭で示した負荷率の式(下式)を活用します。ただし、今回は各需要家ではなく、全需要家をまとめて考えなければなりません。

ここで、分子である「平均需要電力」については、設問(a)ですでに3需要家の総需要電力量[kW・h]を求めているので、これを24[h]で割るだけで求めることができます。
![]()
一方、分母の「最大需要電力」については、負荷率の式(下式)を使って計算します。

不等率は問題の表で1.25(125%)と与えられていて、各需要家の最大需要電力は設問(a)でも解説したように、設備容量と需要率(設備容量に対する最大需要電力)の積で求めることができます。
よって、最大需要電力は以下のように計算できます。

以上から、3需要家をまとめたときの平均需要電力が682[kW]で、最大需要電力が928[kW]だとわかったので、総合負荷率は次のように求めることができます。
![]()
よって、正解は(4)です。

コメント