問 題
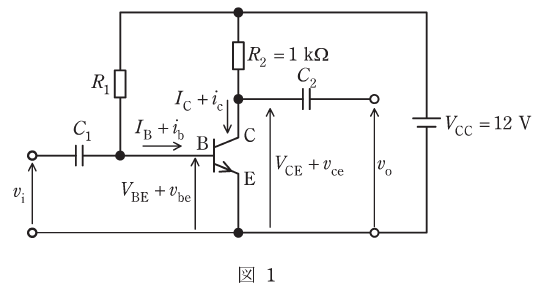
図1に示すエミッタ接地トランジスタ増幅回路について、次の(a)及び(b)の問に答えよ。
ただし、IB[μA]、IC[mA]はそれぞれベースとコレクタの直流電流であり、ib[μA]、ic[mA]はそれぞれの信号分である。
また、VBE[V]、VCE[V]はそれぞれベース-エミッタ間とコレクタ-エミッタ間の直流電圧であり、vbe[V]、vce[V]はそれぞれの信号分である。
さらに、vi[V]、vo[V]はそれぞれ信号の入力電圧と出力電圧、VCC[V]はバイアス電源の直流電圧、R1[kΩ]とR2[kΩ]は抵抗、C1[F]、C2[F]はコンデンサである。
なお、R2＝1kΩであり、使用する信号周波数においてC1、C2のインピーダンスは無視できるほど十分小さいものとする。
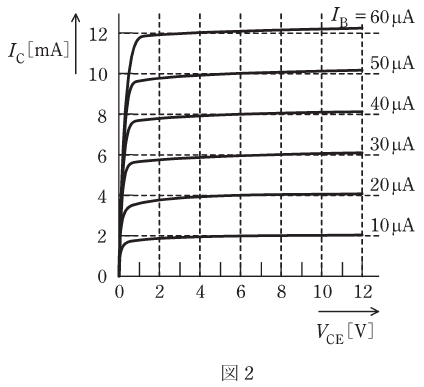
(a) 図2はトランジスタの出力特性である。トランジスタの動作点を
に選ぶとき、動作点でのベース電流IBの値[μA]として、最も近いものを次の(1)～(5)のうちから一つ選べ。
- 20
- 25
- 30
- 35
- 40
(b) 小問(a)の動作点において、図1の回路に交流信号電圧viを入力すると、最大値10μAの交流信号電流ibと小問(a)の直流電流IBの和がベース(B)に流れた。このとき、図2の出力特性を使って求められる出力交流信号電圧vo(＝vce)の最大値[V]として、最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし、動作点付近においてトランジスタの出力特性は直線で近似でき、信号波形はひずまないものとする。
- 1.0
- 1.5
- 2.0
- 2.5
- 3.0
解 説
(a)
求めたいのはIBの値であり、問題文からも図2を使うことは明白です。図2はトランジスタの出力特性の図ですが、ここには直流負荷線が書かれていません。そのため、まずはこの図に直流負荷線を描くことが当面の目的となります。
直流負荷線とは、コレクタ-エミッタ間電圧VCEとコレクタ電流ICとを結ぶ直線のことで、回路図(図1)からキルヒホッフの第二法則を用いることで求めることができます。
ここで、問題の図1がちょっと複雑であるので、これを簡略化した等価回路に描き直してから考えます。
2つのコンデンサは回路としてつながっていないので考えなくてよく、また、トランジスタの部分は図1に記入されているようにVBEとVCEという2つの直流電源に分けます。交流信号分のibやvceなどは(a)では関係なさそうなので、ここではいったん省略し、直流分のみを考えます。
すると、図1は下図のように描き換えることができます。
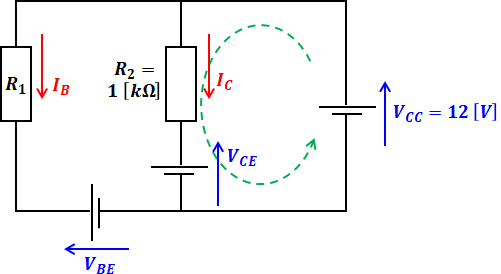
上図の緑色の線で示した閉回路についてキルヒホッフの第二法則を適用すると、以下の式ができあがり、VCEとICの関係式を導けます。これが直流負荷線を表す式となります。
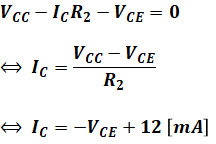
この式(一次関数)を図2に合わせたのが、下図の青色の直線です。
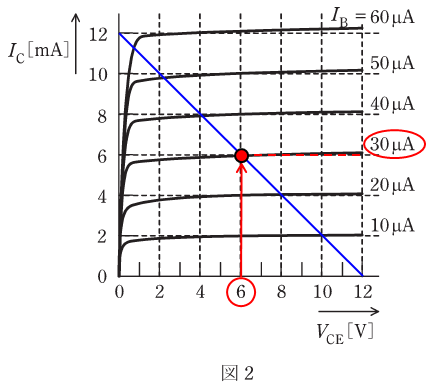
図2に最初から描かれているVCE-IC特性と、自分で記入した直流負荷線との交点を動作点といいます。動作点は複数ありますが、今回はVCE＝6[V]のところなので、上図の赤色で示した矢印をたどることにより、IBの値が30[μA]になることがわかります。
よって、正解は(3)となります。
(b)
(b)の設問でも(a)の動作点での話になるので、(a)で描いた図を引き続き使えます。そこで、先ほどの図を再度示しておきます。
上図より、Ibは30[μA]であり、問題文よりこれに付随する交流信号ibが最大で10[μA]ということなので、直流分は固定で30[μA]、交流分は最大10[μA]と最小－10[μA]の間を変動するので、ベース(B)に流れる電流は30±10[μA]となり、20～40[μA]であることがわかります。
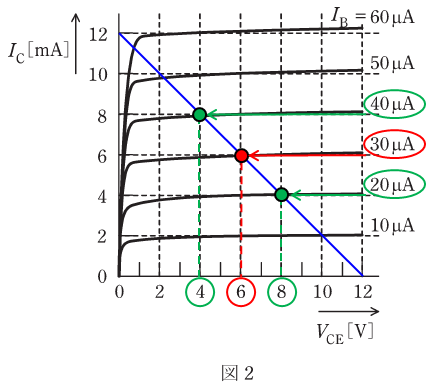
すると、上図の緑色で示したように、交流分を含んだIb(Ib＋ib)が20～40[μA]で変動するとき、交流分を含んだVCE(VCE＋vce)が4～8[V]の間を変動することがわかります。
ここで、問われているのは出力交流信号電圧vo(＝vce)の最大値[V]です。上記より、VCE＋vceの最大値が8[V]であり、VCEは6[V]で固定なので、vceの最大値は2[V]となります。
以上から、正解は(3)です。
コメント