問 題
次の文章は、回転界磁形三相同期発電機の無負荷誘導起電力に関する記述である。
回転磁束を担う回転子磁極の周速をv[m/s]、磁束密度の瞬時値をb[T]、磁束と直交する導体の長さをl[m]とすると、1本の導体に生じる誘導起電力e[V]は次式で表される。
極数をp、固定子内側の直径をD[m]とすると、極ピッチτ[m]は
であるから、f[Hz]の起電力を生じる場合の周速vは
である。したがって、角周波数ω[rad/s]を
として、上述の磁束密度瞬時値b[T]を
と表した場合、導体1本あたりの誘導起電力の瞬時値e(t)は、
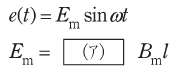
となる。
また、回転磁束の空間分布が正弦波でその最大値がBmのとき、1極の磁束密度の( イ )B[T]は
であるから、1極の磁束Φ[Wb]は
である。したがって1本の導体に生じる起電力の実効値は次のように表すことができる。
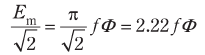
よって、三相同期発電機の1相あたりの直列に接続された電機子巻線の巻数をNとすると、回転磁束の空間分布が正弦波の場合、1相あたりの誘導起電力(実効値)E[V]は、
となる。
さらに、電機子巻線には一般に短節巻と分布巻が採用されるので、これらを考慮した場合、1相あたりの誘導起電力Eは次のように表される。
ここでkwを( エ )という。
上記の記述中の空白箇所(ア)～(エ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。
- ア イ ウ エ
- 2τf 平均値 2.22 巻線係数
- 2πf 最大値 4.44 分布係数
- 2τf 平均値 4.44 巻線係数
- 2πf 最大値 2.22 短節係数
- 2τf 実効値 2.22 巻線係数
解 説
( ア )に関して、これより手前の問題文で提示された条件を反映させると、最初のe＝vblの式は次のように書き換えることができます。
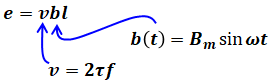
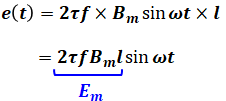
これを( ア )を含む式を見比べると、( ア )には「2τf」が入ることがわかります。
( イ )には「平均値」、「最大値」、「実効値」のいずれかが入りますが、最大値Bmに対してが問われているので、Bが最大値であるわけがありません。よって、実質的に「平均値」と「実効値」の2択です。
正弦波(sinカーブ)の最大値をBmaxとしたとき、その平均値Baveと実効値Beffは次のように表すことができます。
これは重要知識として押さえておきたいところです。詳しくは、「正弦波交流の波形と平均値・実効値」のページを参照してください。
よって、( イ )には「平均値」が入ります。
( ウ )と( エ )に関して、同期機の1相あたりの内部誘導起電力(相電圧実効値)は公式として覚えておきたい知識です。これは、以下のように表されます。
- E：内部誘導起電力 [V] (1相あたりの相電圧実効値)
- kw：巻線係数
- f：周波数 [Hz]
- Φ：磁束 [Wb] (1極あたり)
- N：巻数 (1相あたり)
よって、( ウ )には「4.44」が、( エ )には「巻線係数」が入ります。
ちなみに、もしこの公式を知らない場合でも( ウ )を求めることは可能です。それまでの問題文によると、1本の導体に生じる起電力の実効値が2.22fΦであり、ここでは巻線Nの場合の1相あたりの誘導起電力(実効値)E[V]がいくらになるかが問われています。
ここで、下図を見るとわかるように、巻線1巻きに対して誘導起電力を生じる箇所は2辺分あります。よって、1本の導体に生じる起電力の実効値が2.22fΦなら、巻線Nは導体2N本分になるので、その誘導起電力は4.44fΦNになります。
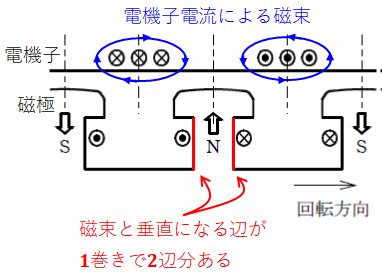
よって、( ウ )には「4.44」が入ると判断できます。
また、( エ )のほうは問題文に「電機子巻線には一般に短節巻と分布巻が～」とあるので、( エ )に「短節係数」や「分布係数」といった一方の言葉が入るのは不適切であると判断できます。これら両方を合わせた用語である「巻線係数」を入れるのが適切です。
以上から、正解は(3)となります。
コメント