問 題
界磁に永久磁石を用いた小形直流発電機がある。回転軸が回らないよう固定し、電機子に3Vの電圧を加えると、定格電流と同じ1Aの電機子電流が流れた。次に、電機子回路を開放した状態で、回転子を定格回転数で駆動すると、電機子に15Vの電圧が発生した。
この小形直流発電機の定格運転時の効率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、ブラシの接触による電圧降下及び電機子反作用は無視できるものとし、損失は電機子巻線の銅損しか存在しないものとする。
- 70
- 75
- 80
- 85
- 90
解 説
最初の条件を回路図に描くと、下図のように表すことができます。回路図の左側が直流発電機、右側が外部電源です。
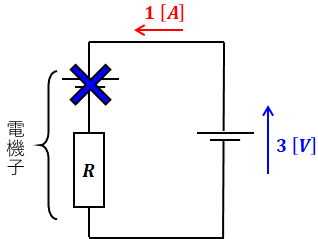
発電機は回転軸が固定されているので発電できません(=電圧が発生しない)が、電流が流れる以上、電機子巻線の損失(銅損)は生じます。よって、上図において左側の電圧源には×をしていますが、抵抗はそのまま残ります。
上図より、抵抗Rの端子電圧は3[V]で、そこを流れる電流は1[A]なので、オームの法則より、抵抗Rの値は3[Ω]となります。
続いて、問題文の後半を踏まえて定格運転時の回路図を考えると、次のように図示できます。電機子回路を開放した状態での端子電圧が15[V]なので、定格運転時の電機子電圧も15[V]となります。また、定格電流は問題文より1[A]です。
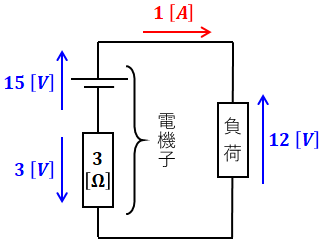
上図において、電機子電圧は15[V]ですが、電機子巻線の銅損が3[V]あるため、出力側の負荷の端子電圧は差し引きで12[V]と計算できます。
ここで、問われているのは発電機の定格運転時の効率です。つまり、電機子で発電した電力[W]のうち、いくらを仕事として取り出せるか(=出力側の負荷の電力[W])という話になります。
よって、次に示すように電機子での発電電力Ptotal、負荷での仕事量Pworkを求めてその割合を出せば、それが効率ηの値となります。
![]()
![]()
![]()
以上より、正解は(3)です。

コメント