問 題
図のように、平らで十分大きい導体でできた床から高さh[m]の位置に正の電気量Q[C]をもつ点電荷がある。次の(a)及び(b)の問に答えよ。
ただし、点電荷から床に下ろした垂線の足を点O、床より上側の空間は真空とし、床の導体は接地されている。真空の誘電率をε0[F/m]とする。
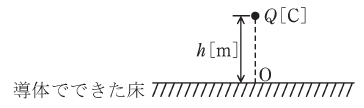
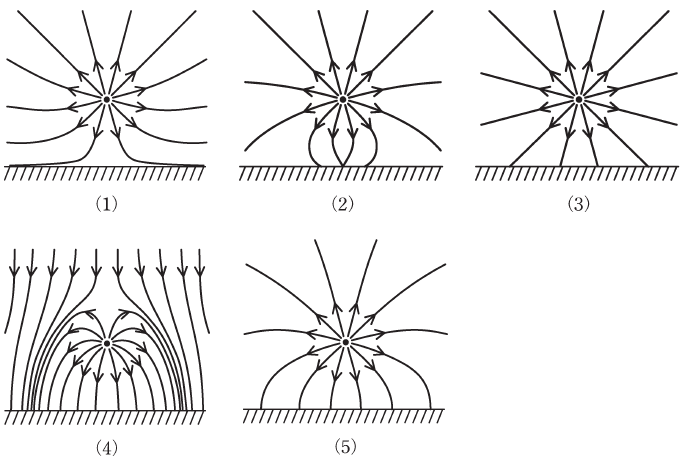
(a) 床より上側の電界は、点電荷のつくる電界と、床の表面に静電誘導によって現れた面電荷のつくる電界との和になる。床より上側の電気力線の様子として、適切なものを次の(1)~(5)のうちから一つ選べ。
(b) 点電荷は床表面に現れた面電荷から鉛直方向の静電吸引力F[N]を受ける。その力は床のない状態で点Oに固定した電気量-Q/4[C]の点電荷から受ける静電力に等しい。
F[N]に逆らって、点電荷を高さh[m]からz[m](ただしh<z)まで鉛直方向に引き上げるのに必要な仕事W[J]を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
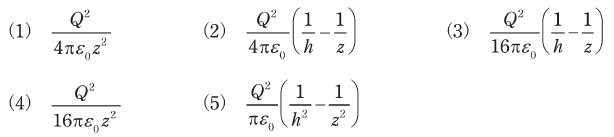
解 説
(a)
(a)の問題文に「床より上側の電界は、点電荷のつくる電界と、床の表面に静電誘導によって現れた面電荷のつくる電界との和になる」と書かれているので、ここでは点電荷の電界と面電荷の電界を分けて考えるとわかりやすいと思います。
まずは「点電荷のつくる電界」について考えると、正電荷を中心として放射状に電気力線が出ていきます(もし負電荷だったら、放射状の電気力線が中心の負電荷に向かう方向となります)。つまり、次の図のような感じになります。
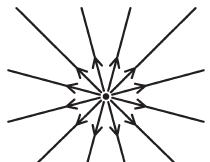
これは選択肢(3)の形と同じです。よって、(3)は「点電荷のつくる電界」だけを示す図となっていて、「床の表面に静電誘導によって現れた面電荷のつくる電界」の分が足りません。
そこで、続いて「床の表面に静電誘導によって現れた面電荷のつくる電界」について考えますが、その前に静電誘導という言葉を整理しておきます。
真空中において、正に帯電した帯電体(正電荷)を帯電していない絶縁された導体に近づけると、導体の帯電体に近い側の表面付近に負の電荷が現れます。この現象が静電誘導です。
つまり、今回の場合は問題の図の上側に正電荷、床に導体があるため、床表面全体が負電荷に帯電するということになります。
よって、電気力線は負電荷のほうに向かっていく矢印で表現できるため、「床の表面に静電誘導によって現れた面電荷のつくる電界」は次のように図示できます。
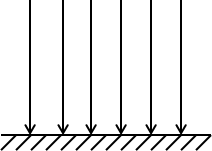
以上から、上図の2つを組み合わせたものが答えとなります。初めに正電荷があって、その影響を受けて静電誘導が生じているので、電界の強さでいえば「点電荷のつくる電界」のほうが強いです。
よって、「点電荷のつくる電界」として示した放射状の電気力線の図を基本として、「床の表面に静電誘導によって現れた面電荷のつくる電界」である下向きの矢印の影響が加わるので、これらを合わせた電界は次のように表現できます。
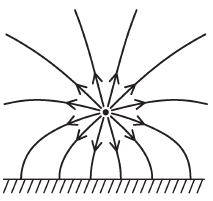
以上から、「床より上側の電界」は(5)の図が該当します。
(b)
この問題は仕事Wが問われていますが、単位電荷(1クーロンの電荷を持つ点電荷)をある場所から別の場所まで移すために要する仕事のことを電位Vといいます。
電位Vは以下の式で表すことができます。これは重要公式としてぜひ押さえておきたい知識です。
![]()
- V:電位 [V]
- ε0:真空の誘電率 8.854×10-12 [F/m]
- Q:電荷 [C]
- r:点電荷からの距離 [m]
ただし、電位Vというのは上記の通り単位電荷あたりの仕事のことなので、全体としての仕事Wを計算するには、これに移動する電荷Q’を掛ける必要があります。つまり、仕事Wは次の式で表すことができます。
![]()
今回の場合は2つの点電荷(正確には点電荷と面電荷ですが、面電荷は問題文の通り点電荷に換算しています)がQと-Q/4です。また、点電荷の距離は最初h[m]だったところから、z[m]の距離に移動しています。
よって、距離がhのときのWhと距離がzのときのWzをそれぞれ計算して、移動後のWzから移動前のWhを引いた値が求めたいWということになります。
つまり、仕事Wは次のように計算することができます。
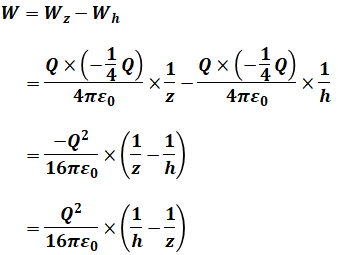
以上から、正解は(3)となります。

コメント