問 題
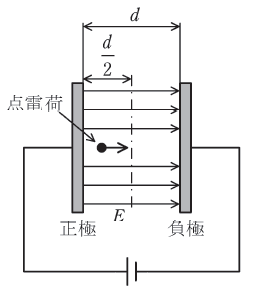
図のように、極板間の距離d[m]の平行板導体が真空中に置かれ、極板間に強さE[V/m]の一様な電界が生じている。
質量m[kg]、電荷量q(>0)[C]の点電荷が正極から放出されてから、極板間の中心d/2[m]に達するまでの時間t[s]を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、点電荷の速度は光速より十分小さく、初速度は0m/sとする。また、重力の影響は無視できるものとし、平行板導体は十分大きいものとする。
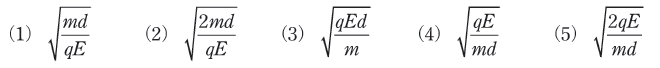
解 説
真空中に点電荷があり、もしそこに電界または磁界が存在するなら、この点電荷に力が働いて点電荷は運動します。より具体的には、電界中では点電荷は等加速度運動をし、磁界中では点電荷は円運動をします。
つまり、この問題は電界中の話なので点電荷は等加速度運動をするのですが、以下ではそのことを式を使いながら説明していきます。
まず、今回は質量m[kg]、電荷量q[C]の点電荷が正極から放出されるという運動なので、次に示す運動方程式が成り立ちます。
![]()
- F:静電気力 [N]
- m:点電荷の質量 [kg]
- a:点電荷の加速度 [m/s2]
一方、静電気力F[N]は、電荷量q[C]と電界E[V/m]との積で表すことができるので、上記の運動方程式は次のように書き換えることができます。
![]()
- q:電荷[C]
- E:電界[V/m]
これを加速度aについて解くと、
![]()
となり、上式の右辺のパラメータ(q、E、m)は全て定数なので、加速度aは一定であることがわかります。よって、この電子の運動は等加速度運動であるといえます。
また、等加速度運動であることがわかれば、速度v[m/s]や距離x[m]は時間t[s]を使って次のように表すことができます。
速度vを表す式![]()
距離xを表す式![]()
よって、今回は距離x=d/2であることがわかっているので、上式下側に諸々の数値を当てはめていけば、求めたい時間tの値が得られます。ちなみに、初速度v0=0であるという条件は問題文に記載されています。
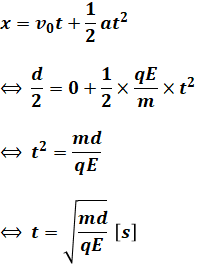
以上から、正解は(1)です。

コメント