問 題
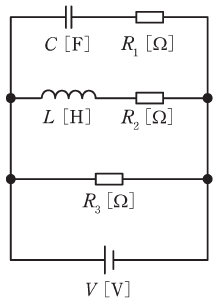
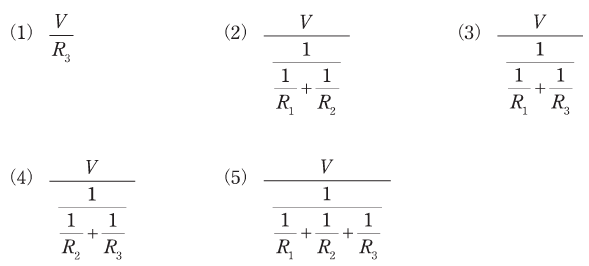
図のように、三つの抵抗R1[Ω]、R2[Ω]、R3[Ω]とインダクタンスL[H]のコイルと静電容量C[F]のコンデンサが接続されている回路にV[V]の直流電源が接続されている。定常状態において直流電源を流れる電流の大きさを表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
解 説
一般論として、抵抗、コイル、コンデンサのうち、抵抗はスイッチを入れた直後でも定常状態でも常に同じような働きをしますが、コイルとコンデンサはそうではありません。
コイルについて、電流が流れ始めた瞬間のコイルの両端の電位差は大きく、電流は全然流れません。その後、徐々に電位差が小さくなり(=電流が大きくなっていき)、充分な時間が経ったあとのコイルは、その両端の電位差が0になります。
よって、コイルに関しては、電流が流れた瞬間は「開放」で、定常状態では「短絡」しているものと見なすことができます。
コンデンサはコイルとは対称的で、回路をつないだ直後は電流が流れてコンデンサに電荷が溜まっていきますが、流れる電流は徐々に小さくなっていき、定常状態に達したあとは全く流れなくなります。
よって、コンデンサに関しては、電流が流れた瞬間は「短絡」で、定常状態では「開放」しているものと見なすことができます。
以上を踏まえると、問題の回路図は次のように描き換えることができます。
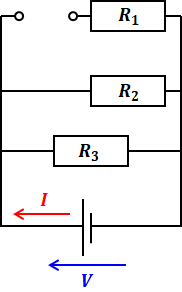
よって、上側のR1は回路がつながっていないので電流が流れません。そのため、この回路はR2とR3との並列回路になるため、合成抵抗RはR2、R3を使って次のように表すことができます。
ちなみに、実は選択肢(1)~(5)の中でR2、R3を使ってR1を使わないのが(4)だけなので、この時点で正解は(4)だと推測できます。ここでは解説の続きをしますが、本番の試験ではこの時点で次の問題に進んでもよいと思います。
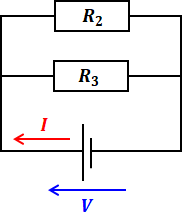
![]()
上式は通分して逆数を取ることでR=~の形に直すことができますが、選択肢(1)~(5)の表記がこの形になっているので、計算せずにそのままにしておきます。
以上から、電源を流れる電流Iは以下のように計算できます。
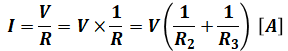
本来ならこれで正解の選択肢を選びたいところですが、今回の場合だと選択肢に当てはまるものがありません。選択肢(2)~(5)は三重の分数になっているので、これに合わせて上式を変換します。ちなみに、(1)は普通の分数ですが、これは上記の計算結果と合っていないので不適です。
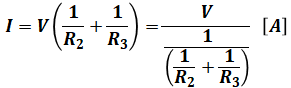
よって、正解は(4)となります。

コメント