問 題
論理関数について、次の(a)及び(b)の問に答えよ。
(a) 論理式![]() を積和形式で簡単化したものとして、正しいものを次の(1)~(5)のうちから一つ選べ。
を積和形式で簡単化したものとして、正しいものを次の(1)~(5)のうちから一つ選べ。
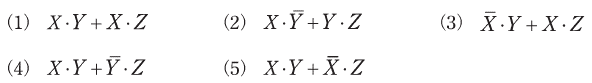
(b) 論理式![]() を和積形式で、簡単化したものとして、正しいものを次の(1)~(5)のうちから一つ選べ。
を和積形式で、簡単化したものとして、正しいものを次の(1)~(5)のうちから一つ選べ。
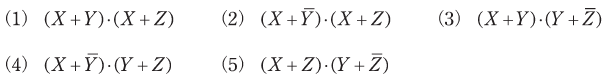
解 説
(a)
問題の論理式は、XYZのセットが4セットありますが、1項目と3項目、2項目と4項目はそれぞれ、3成分のうち2成分が共通であるため、以下のようにくくることができます。
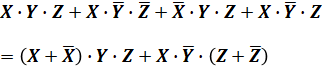
ここで、上記の計算結果の左側の( )内は、「XであるものとXじゃないもの」の和なので、つまりは全て(=1)です。右側の( )のZについても同様です。
よって、計算結果は以下の通りとなります。
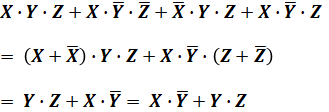
以上から、正解は(2)です。
(b)
ちゃんとした解説も以下で示しますが、その前に、この問題に限っては細かい計算をせずに答えが出せるので、まずはその考え方を紹介します。
問題で与えられた論理式では、YとZは等価であることがわかります。つまり、YとZを入れ替えても全く同じ論理式になる、ということです。ということは、この論理式を簡単化した結果である答えの式もYとZが等価であるはずです。
ここで選択肢を見ると、(2)ではYにバーが付いているのに対してZにはバーが付いていないので、これは等価とはいえません。また、(3)、(4)、(5)に関してはYとZの数が違うので、やはりこれもYとZが等価ではありません。
よって、この問題の答えはYとZが等価に配置されている(1)であると判断できます。
このような判断で答えを出せると、計算時間を大きく減らすことができるのでお勧めです。
ただし、今回はたまたま都合の良い選択肢だっただけなので、この方法で必ず答えが出せるわけではありません。なので、以下に示すきちんとした解法もぜひ身につけてください。
問題で与えられた論理式は( )の中が和になっていて、( )同士を積でつなぐ形になっています。しかし、(a)のような形、つまり、( )内を積にして、( )同士を和でつなぐと、(a)と同様に共通部分をくくって整理できるので、式を簡単化するためにはこちらのほうが便利です。
よって、この論理式全体に二重のバーを付けて(二重否定は逆の逆なので元の論理式とイコールになります)、その上で「+」のバーを「・」に、「・」のバーを「+」に変換すると、次のような式になります。
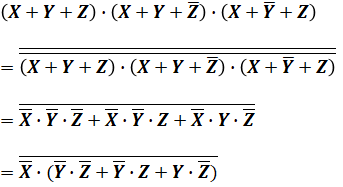
ここで、( )内の部分は、「YでなくZでもない」と「YでなくてZである」と「YであってZではない」の和なので、これは「YでありZでもある」の否定(バー)として次のようにまとめることができます。
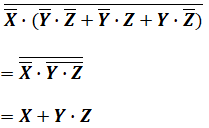
よって、これが正解…と言いたいところですが、上式と合致するものが選択肢にはないため、ブール代数の分配則を使ってさらに変換させると、求める答えが得られます。
![]()
以上から、正解は(1)とわかりますが、もしこの変換がわかりにくいと感じる場合は、むしろ選択肢の式を展開したほうがわかりやすいかもしれません。
「X+Y・Z」までは確定しているので、選択肢の中で否定(バー)が付いていない選択肢(1)が正しそうだと目星を付けて展開してみると、次のようになります。

そうすると、確かに選択肢(1)が「X+Y・Z」であると確認できるため、これが正しいと判断することができます。
以上から、正解は(1)となります。

コメント