電験三種 R1年 機械 問16 問題と解説

　問題　　　　　

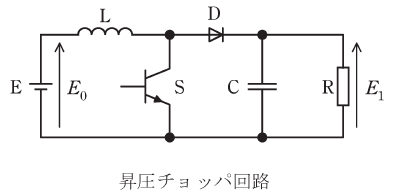
図は直流昇圧チョッパ回路であり、スイッチングの周期をT[s]とし、その中での動作を考える。ただし、直流電源Eの電圧をE₀[V]とし、コンデンサCの容量は十分に大きく出力電圧E₁[V]は一定とみなせるものとする。

半導体スイッチSがオンの期間T_on[s]では、E－リアクトルL－S－Eの経路とC－負荷R－Cの経路の二つで電流が流れ、このときにLに蓄えられるエネルギーが増加する。

Sがオフの期間T_off[s]では、E－L－ダイオードD－(CとRの並列回路)－Eの経路で電流が流れ、Lに蓄えられたエネルギーが出力側に放出される。次の(a)及び(b)の問に答えよ。

(a)　この動作において、Lの磁束を増加させる電圧時間積は(　ア　)であり、磁束を減少させる電圧時間積は(　イ　)である。定常状態では、増加する磁束と減少する磁束が等しいとおけるので、入力電圧と出力電圧の関係を求めることができる。

上記の記述中の空白箇所(ア)及び(イ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

(b)　入力電圧E₀=100V、通流率α=0.2のときに、出力電圧E₁の値[V]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

正解 (a)-(1), (b)-(2)

　解説　　　　

問題文にある通り、スイッチがオンのときには回路を流れる電流は下図の赤矢印のように表されます。

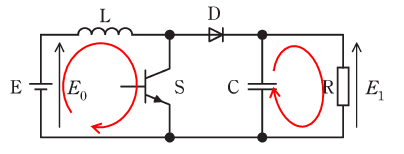
上図左側(E－L－S)を見るとわかるように、これは電圧EとリアクトルL、スイッチSだけで成り立つ回路なので、リアクトルLの端子間電圧はE₀[V]となります。

「Lの磁束が増加」と「Lに蓄えられるエネルギーが増加」は同義なので、Lの磁束を増加させる電圧時間積を問われたら、電圧はE₀[V]、時間はT_on[s]より、E₀・T_onと答えることができます。

また、スイッチがオフのときには回路を流れる電流は下図の赤矢印のように表されます。

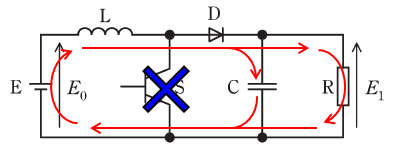
ダイオードでは電圧の増減がないため、上図においてリアクトルLの端子間電圧は、出力電圧E₁[V]と電源電圧E₀[V]の差(E₁－E₀)[V]となります。

「Lの磁束が減少」と「Lに蓄えられるエネルギーが放出」は同義なので、Lの磁束を減少させる電圧時間積は、電圧(E₁－E₀)[V]、時間T_off[s]より、(E₁－E₀)・T_offとなります。

以上より、正解は(1)です。

(a)の問題文にも書かれているように、定常状態では、増加する磁束と減少する磁束が等しくなります。そして、その磁束の増減を数値化した電圧時間積をすでに(a)で求めているので、これを利用すると以下の等式が成り立ちます。

よって、この等式をE₁について解けば求める答えが得られます。

ただし、T_onとT_offは問題文で与えられず、その代わりに通流率αが与えられています。通流率は、全体の時間Tのうちのスイッチオンの時間T_onの割合なので、ここではT_on＝0.2T、T_off＝0.8Tのようにしておけばよいです。

以上を踏まえると、次のように計算を進めることができます。

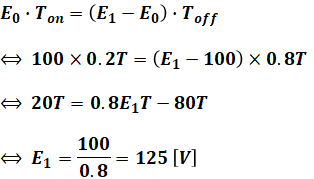
よって、正解は(2)となります。

電験三種 R1年機械問16 問題と解説